1. Математика
  2. Мистер фокс записал на

Мистер фокс записал на доске число (9*15-1)^2019 . предварительно посчитав сумму цифр этого числа, мистер фокс стер число с доски и записал вместо него сумму цифр. он продолжал повторять эту операцию до тех пор, пока на доске не осталось однозначное число. какое число осталось на доске?

dianamakhmutova1 dianamakhmutova1    3   01.02.2020 20:03    4

Ответы
Ardashelovna Ardashelovna  11.10.2020 04:10

Пусть S(n) - сумма цифр натурального числа. Докажем, что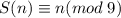 S(n)\equiv n(mod \;9)

Пусть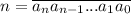 n=\overline{a_na_{n-1}...a_1a_0}. Тогда

n=a_n*10^n+a_{n-1}*10^{n-1}+...+a_1*10^1+a_0*10^0=a_n*(9+1)^n+a_{n-1}*(9+1)^{n-1}+...+a_1*(9+1)^1+a_0\equiv a_n*1^n+a_{n-1}*1^{n-1}+...+a_1*1^1+a_0(mod\;9)=a_n+a_{n-1}+...a_1+a_0=S(n)

Доказано.

Тогда очевидно, что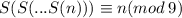 S(S(...S(n)))\equiv n(mod\: 9), и оставшееся в конце однозначное число дает при делении на 9 тот же остаток, что и исходное число.

(9*15-1)^{2019}\equiv(-1)^{2019}(mod\;9)=-1\equiv 8(mod\;9)

Единственное однозначное число, дающее остаток 8 при делении на 9, - это 8.

ответ: 8

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
BOT1111111 BOT1111111  17.04.2020 13:46
А) 3 (5х+7)=18; б)5х-3 (3х-7)=35; в)(х-4)(2.3-4.6х)=0;...
pro22896 pro22896  17.04.2020 13:46
на клетчатом поле со стороной клетки 1 см изображён треугольникнайдите площадь этого треугольника проведи на рисунке выше прямую линию так, чтобы этот прямоугольник оказался разбит...
Leonelle Leonelle  17.04.2020 13:46
Найди значение выражения: 14 · √18 · 5 · √3 · √54...
imam002121 imam002121  17.04.2020 13:46
Укажите равенство, в котором правильно выполнена подстановка системы {x=3y-7 {2x+3y=1 . 1) 2y+3(3y-7)=1 2) 2(3y+7)+3y=1 3) 2y+3(3y+7)=1 4) 2(3y-7)+3y=1...
Рооопапооугвр Рооопапооугвр  17.04.2020 13:46
В правильной треугольной пирамиде высота боковой грани равна 26см,а высота пирамиды 24 см.Найдите объём пирамиды...
tarasgorodchukowd1fp tarasgorodchukowd1fp  17.04.2020 13:46
Составь выражение по условию задачи: Лиза бежит со скоростью 10 км/ч. Сколько километров она пробежит за х часов?​...
Terbull Terbull  17.04.2020 13:46
я не знаю как сделать х, если х =0,08...
kamilatoktorbel kamilatoktorbel  17.04.2020 13:30
поскорее, очень нужно (решать подробно) ​...
максим1722 максим1722  17.04.2020 13:46
Составь уравнение к задаче, начало решения которой выглядит так:1-я пачка 2-я пачка2Было тетрадейСтало тетрадей | 2x — 16x + 29Известно, что количество тетрадей, получившихся в каждой...
nikita1424 nikita1424  20.05.2019 04:30
Сколько процентов состовляет: 5 кг от 100кг 6 т от 30 т 4,5 г от 30 г 2.8 кг от 7 км 1.2м от 6 м 9.6 м от 24 м...

Популярные вопросы