Миша и 8 его друзей хотят разделиться на 3 команды по 3 человека. Сколькими различными они это могут сделать? У команд нет номеров, поэтому два разбиения на команды считаются
разными, если хотя бы два сокомандника в одном разбиении не являются сокомандниками в
другом.

Ответы

SuperZadrot200 10.03.2022 17:10

Решать задачу будем в два этапа: сначала определим число разбить друзей на 3 пронумерованные команды, а затем учтем, что эта нумерация не важна.

1. Формируем первую команду. Туда должны попасть некоторые 3 человека из 9. Порядок их выбора не важен, поэтому выбрать их можно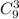 C_9^3 .

Формируем вторую команду. Туда должны попасть некоторые 3 человека из оставшихся 6. Порядок их выбора также не важен, поэтому выбрать их можно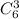 C_6^3 .

Оставшиеся 3 человека автоматически сформируют третью команду.

Поскольку каждому варианту первой команды можно поставить в соответствие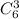 C_6^3 вариантов второй (и третьей) команды, то по правилу умножения всего разбить 9 человек на 3 пронумерованные команды:

$C_9^3\cdot C_6^3$

2. Теперь учтем тот факт, что у команд на самом деле нет номеров. Так как команд 3, то существует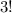 пронумеровать команды. Таким образом, количество непронумерованных вариантов разбиения в 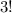раз меньше, чем количество пронумерованных вариантов разбиения.

Значит, итоговое число разбить 9 человек на команды без учета их номеров:

$\dfrac{C_9^3\cdot C_6^3}{3!} =\dfrac{\dfrac{9!}{3!\cdot(9-3)!} \cdot \dfrac{6!}{3!\cdot(6-3)!}}{3!} =\dfrac{9!\cdot 6!}{3!\cdot6!\cdot 3!\cdot3!\cdot3!}=\dfrac{9!}{(3!)^4}=$