Между пунктом а и пунктом в находится пункт с. расстояние между а и в 375км. автомобилист выехал из пункта в в пункт а, спустя 1,5 часа из пункта в выехал мотоциклист за автомобилистом. они встретились в пункте с, после чего мотоциклист направился назад в пункт в, а автомобилист продолжил ехать в пункт а. автомобилист приехал в пункт а одновременно с ним в пункт в приехал мотоциклист. скорость мотоциклиста 75 км в час. найти скорость автомобилиста

1ч30мин=1.5ч

х-скорость автомобиля

t-время в пути мотоциклиста до встречи с автомобилем (из В до С)

t+1.5-время в пути автомобиля до встречи с мотоциклистом (из В до С)

t=1.5x/(75-x)

х*t= расстояние из С в А, которое проехал автомобиль

375-75t=расстояние из С в А, которое не проехал мотоциклист

375-75t=xt

xt+75t=375

t(x+75)=375

x+75=375/t

x+75=375:(1.5x/(75-x))

х+75=375*((75-х)/1.5х)

х+75=(28125-375х)/1.5х

28125-375х=1.5х(х+75)

28125-375х=1.5х^2+112.5х

1.5х^2+487.5х-28125=0

Д=237656.25+168750=406406.25

корень из Д=637,5

х1=(-487.5-637.5)/3=-375 не подходит

х2=(-487.5+637.5)/3=50км/ч скорость автомобиля

проверяем:

50*1.5=75км проехал автомобиль за 1ч30мин

75-50=25км/ч скорость сближения

75:25=через 3 часа мотоцикл догнал автомобиль в С

3*75=50(3+1.5)

  225=225км расстояние от В до С

375-225=150км от С до А

150:50=3 часа ехал автомобиль из С до А

225:75=3 часа ехал назад мотоцикл из С в В

3ч=3ч

Пусть x - расстояние от B до C, а t это время, которое потратил на путь из B в C мотоциклист, тогда 1) расстояние от C до A = 375 - x; 2) автомобилист потратил на путь из B в A = 1,5 + t. По условию задачи скорость мотоциклиста 75 км/ч.

V (автомобилиста) =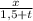 

V (мотоциклиста) = ,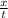

сказанно на путь из C в A (375 - x) автомобилит потратил времени столько же, сколько мотоциклист на путь из C в B (x):

, т.к. x / t = 75, то x = 75t:

D = 49 + 240 = 289 = 17^2

t (1,2) = 3; - 5/4 (не удовлетворяет)

V (автомобилиста) =