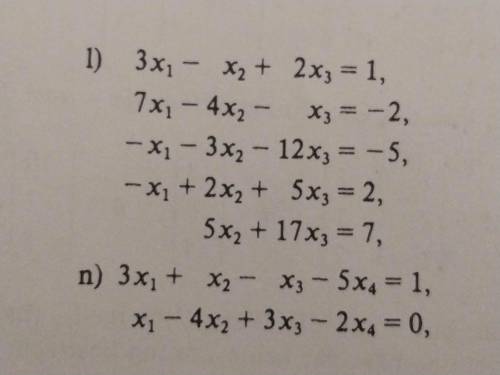
Другие вопросы по теме Математика
DianaSagatbekova
27.08.2019 04:00
Ram543
27.08.2019 04:00
gsergey1
27.08.2019 04:00
Артём00071
27.08.2019 04:00
ritosha002
27.08.2019 04:00
inikulin00864
27.08.2019 04:00
endermeska
27.08.2019 04:00
НезнайкаФдпун
27.08.2019 03:50
Популярные вопросы
- До ть,будь ласка, із завданнямУ лівій частині рівняння 1-х+х^2-х^3+...=3х...
3 - У двох бідонах 54 л.молока,причому в одному з них у 2 рази більше,ніж...
1 - В столярной мастерской работают мастер и его ученик. За сколько дней...
2 - А 7. Яна написала о костюме девушек, но забыла прилагательные Янеподобрать...
1 - Почему всегда необходимо следить за уровнем масла в двигателе автомобиля?...
3 - Груз, подвешенный к динамометру, опускают в стакан с водой до полного...
2 - с историей про Древнюю Грецию 1)запиши понятия: 1. семиструнный музыкальный...
2 - Каково влияние спиртов на организм человека?2.Составить и назвать структурные...
1 - Решите очень в магазине продавалось 127 документальных фильмов 93 исторических...
2 - понять, что за слова нужно вставить вместо пропущенных, а так же отгадать,...
1
P.S. Идет x1 x2 x3 x4 = B
1)
Запишем систему в виде расширенной матрицы:
3 -1 2 1
7 -4 -1 -2
-1 -3 -12 -5
-1 2 5 2
0 5 17 7
Для удобства вычислений поменяем строки местами:
0 5 17 7
-1 -3 -12 -5
-1 2 5 2
3 -1 2 1
7 -4 -1 -2
Умножим 3-ю строку на (-1). Добавим 3-ю строку к 2-й:
0 5 17 7
0 -5 -17 -7
-1 2 5 2
3 -1 2 1
7 -4 -1 -2
Умножим 3-ю строку на (3). Добавим 4-ю строку к 3-й:
0 5 17 7
0 -5 -17 -7
0 5 17 7
3 -1 2 1
7 -4 -1 2
Умножим 4-ю строку на (7). Умножим 5-ю строку на (-3). Добавим 5-ю строку к 4-й:
0 5 17 7
0 -5 -17 -7
0 5 17 7
0 5 17 13
7 -4 -1 -2
Добавим 2-ю строку к 1-й:
0 0 0 0
0 -5 -17 -7
0 5 17 7
0 5 17 13
7 -4 -1 -2
Добавим 3-ю строку к 2-й:
0 0 0 0
0 0 0 0
0 5 17 7
0 5 17 13
7 -4 -1 -2
Умножим 4-ю строку на (-1). Добавим 4-ю строку к 3-й:
0 0 0 0
0 0 0 0
0 0 0 -6
0 5 17 13
7 -4 -1 -2
Для удобства вычислений поменяем строки местами:
0 0 0 0
0 0 0 0
0 0 0 -6
0 5 17 13
7 -4 -1 -2
Система не совместна. Так как при любых вычислениях в каждой строчке почти есть по нулю.
n)
Запишем систему в виде расширенной матрицы:
3 1 -1 -5 1
1 -4 3 -2 0
Умножим 2-ю строку на (-3). Добавим 2-ю строку к 1-й:
0 13 -10 1 1
1 -4 3 -2 0
Теперь исходную систему можно записать так:
Необходимо переменные x3,x4 принять в качестве свободных переменных и через них выразить остальные переменные.
Приравняем переменные x3,x4 к 0
Из 1-й строки выражаем x
Из 2-й строки выражаем x1