Математика задача 9
Сколькими нулями оканчивается сумма 2022!+2023!+2024!+…+9999! ?
Другие вопросы по теме Математика
Популярные вопросы
- 91. решите уравнение б)3,5x+2,2x=4,56...
2 - Напишите мини-сочинение на тему урок языка в публицистическом и художественном...
3 - Урок по биологии эссе на тему зависимость между количеством осадков и...
3 - Точка e , f, k , l соответственно середины сторон ab , bc , cd , da ,...
3 - Допиши окончания существительных общего рода.сделай вывод об особенностях...
1 - Решите (3.5-x): 6=1.2 8 x-3.2=5.6 x-5.2=4.9 y+3.54=8.2...
2 - Іть будь-ласка написати твір-роздум що є свобода? добро в ній яке є?...
3 - Собственная скорость катера равна 26,8 км/ч,а скорость течения реки-2,7...
2 - Культура язык и общение язык в жизни человека найди в тексте слова которые...
2 - Скажите как заполнить таблицу. испанская колония империи и португальская...
3
Вынесем общий множитель за скобку: . Еще вынесем:
. Еще вынесем: 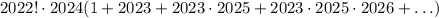 . Теперь видно, что слагаемые дальше
. Теперь видно, что слагаемые дальше  делятся на
делятся на 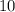 . Сумма первых трех оканчивается на
. Сумма первых трех оканчивается на 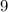 , а потому взаимно проста с десятью. Следовательно, сумма оканчивается на то количество нулей, на которое оканчивается
, а потому взаимно проста с десятью. Следовательно, сумма оканчивается на то количество нулей, на которое оканчивается 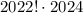 . Двоек в
. Двоек в 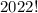 :
: ![\nu_{2}(2022!) = [2022/2]+[2022/2^2]+\ldots = 1011+505+252+126+63+31+15+7+3+1=2014](/tpl/images/4772/6715/7e92f.png) , а пятерок:
, а пятерок: ![\nu_{5}(2022!) = [2022/5]+[2022/25]+\ldots = 404+80+16+3=503](/tpl/images/4772/6715/846c8.png) . Значит сумма есть
. Значит сумма есть 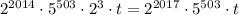 , где
, где 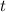 взаимно просто с
взаимно просто с 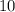 . Тогда сумма оканчивается на
. Тогда сумма оканчивается на 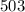 нуля.
нуля.