Математика решить одно уравнение.
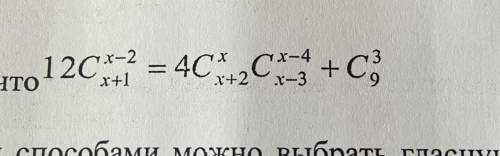
Другие вопросы по теме Математика
Популярные вопросы
- . Подайте у вигляді квадрата двочлена многочлен 4b2+4ab+a2.А: (b+2a)2Б:...
1 - Сделайте формулу оксидов Карбона(2) Карбона(5) Нитрогена(4) Сульфура...
1 - (5 1/4 - 6 1/6) * (3 1/4 - 0,55)=...
1 - Choose and write words in the right columns....
2 - X²+4x-77=0 решите без корней...
1 - Кого з роду кулакивських софйка и виришила врятувати...
2 - Как коростель мигрирует плз!! ☺☺☺☺...
3 - Чому на річках північної півкулі правий берег крутий а лівий положистий...
2 - Длина каждой стороны многоугольникп 9см.периметр этого многоугольникп...
1 - с во к поэме Песня про Гайавата 1. Кто научил охотиться Гайавата?...
3
Відповідь:
С ˣ⁻²ₓ₊₁ = (х+1)! / ((х-2)!(х + 1 - х +2)! )
= (х+1)х(х-1) / 3! = х(х+1)(х-1) / 6,
С ˣ ₓ₊₂ = (х+2)! / х!*2! = (х+2)(х+1) / 2,
Сˣ⁻⁴ₓ₋₃ = х - 3,
С³₉ = 9*8*7 / 6 = 84
Отже, першопочаткове рівняння буде мати вигляд:
12х(х+1)(х-1) / 6 = 4(х+2)(х+1)(х-3) / 2 + 84,
2х³ - 2х = 2(х² + 3х + 2)(х-3) + 84
2х³ - 2х = 2х³ - 18х + 4х -12 + 84
14х - 2х = 72
12х = 72
х = 72 : 12
х = 6