Математик
решить пример из вложения.
С объяснениями
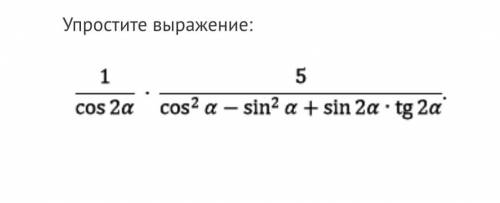
Другие вопросы по теме Математика
Популярные вопросы
- Синтаксический разбор предложения: Рядом расположился мужичонка в...
2 - В цепи, состоящей из последовательно соединенных конденсатора и катушки,...
2 - найти ошибки (всего должно быть 10)...
1 - Hjata - Стрельба-mВыделите корни у глаголов.Просклоняй (по падежам)...
3 - A Cowboys Life by Rozanne Lanczak Williams пересказ на английском...
2 - Дополни текст определениями, подчеркни их волнистой линеей. Определи...
3 - Сущность Конституции – это: А) баланс основных интересов, представленных...
2 - Вследствие плавления ледяной шарики при 0 С, ее радиус уменьшился...
3 - задачи! 4) На экране получено изображения предмета высотой 5 см,...
2 - При каком значении верно равенство: 6/х= 30/35...
1
сos2α=cos²α-sin²α;
tg2α=sin2α/cos2α;
sin²2α+cos²2α=1, поэтому
(1/cos2α)*(5/(cos²α-sin²α+sin2α*tg2α)=
(1/cos2α)*(5/(cos2α+sin2α*sin2α/cos2α))=(1/cos2α)*(5/(cos2α+sin²2α/cos2α))=
(1/cos2α)*(5/((cos²2α+sin²2α)/(cos2α)))=5*cos2α/cos2α=5
ответ 5
5
Пошаговое объяснение:
используя формулы тригонометрии cos²a-sin²a=cos2a
tg2a=sin2a/cos2a,
и преобразуя выражение, получаем
1/ cos2a × 5 / (cos2a +sin2a × sin2a / cos2a ) = 1/ cos2a × 5 / (cos2a + sin²2a/cos2a) = 1/cos2a × 5 / [(cos²2a+sin²2a)/cos2a] = 1/cos2a × 5/ (1/cos2a)= 1/cos2a × 5cos2a= 5