Мат анализ Складіть рівняння дотичної площини та нормалі до
поверхні z(x,y) у точці M:
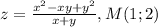
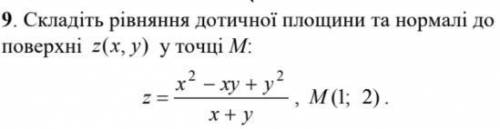
Другие вопросы по теме Математика
Популярные вопросы
- в одному бідоні а л,а в іншому б літрів молока.у перший бідон додали 4 л...
3 - на диаграмме представлена информация о покупках, сделанных в интернет-магазинах...
2 - Казак тылы 6 сынып 3 тапсырма 179 бет...
3 - .твір Прилетіла ластівка , використовуючи складні речення...
3 - Глупый Письмо само Никуда не пойдет.Но в ящик его опусти -Оно пробежит,Пролетит,Проплывети...
3 - Твір Рей Бредбері Все літо в один день написати твір 100-110 слів про те,...
2 - 504. Вычислите удобным а) 2,5 1,03 4:б) 0,5 - 79,6 2: в) 0.25 0.5 2.4.г)...
3 - 36. Найдите:3% от 400;9% от 250;25% от 18:50% от 70...
2 - Написати 100-120 слів про бачення людини сонця. 3 завдання,на 14:20 хвилині....
3 - Решить задачи: 1. Должник вернул две пятых долга - 6000 рублей. Какую сумму...
1
Шаг 1: Найдите значения функции z(x,y) в точке M(1,2)
Подставим координаты точки M(1,2) в уравнение поверхности z(x,y):
z(1,2) = (1^2 - 1*2 + 2^2)/(1+2) = (1-2+4)/3 = 3/3 = 1
Таким образом, значение функции z равно 1 в точке M(1,2).
Шаг 2: Найдите частные производные функции z(x,y) по x и y
Возьмем производную функции z(x,y) по x, считая y постоянной:
∂z/∂x = (2x - y)/(x+y)^2
Возьмем производную функции z(x,y) по y, считая x постоянной:
∂z/∂y = (-x + 2y)/(x+y)^2
Шаг 3: Найдите нормальный вектор к поверхности
Нормальный вектор к поверхности это вектор, перпендикулярный к дотичной плоскости. Он имеет координаты, соответствующие значениям ∂z/∂x и ∂z/∂y в точке M(1,2).
Таким образом, нормальный вектор будет иметь координаты (2(1) - 2)/(1+2)^2, (-1 + 2(2))/(1+2)^2.
Вычислим значения:
Нормальный вектор = (-1)/(3^2), (3)/(3^2) = (-1/9, 1/3)
Шаг 4: Найдите уравнение дотичной плоскости
Уравнение дотичной плоскости имеет вид:
z - z0 = (∂z/∂x, ∂z/∂y) • (x - x0, y - y0)
Подставим значения в уравнение:
z - 1 = (∂z/∂x, ∂z/∂y) • (x - 1, y - 2)
Учитывая, что (∂z/∂x, ∂z/∂y) = (∂z/∂x, ∂z/∂y) / ∥(∂z/∂x, ∂z/∂y)∥, получим:
z - 1 = ((2(1) - 2)/(1+2)^2, (-1 + 2(2))/(1+2)^2)/(√((-1/9)^2 + (1/3)^2)) • (x - 1, y - 2)
Распишем:
z - 1 = ((0)/(9), (1))/(√((-1/9)^2 + (1/3)^2)) • (x - 1, y - 2)
z - 1 = (0, 3)/(√((1/9) + (1/9))) • (x - 1, y - 2)
z - 1 = (0, 3)/(√(2/9)) • (x - 1, y - 2)
z - 1 = (0, 3)/(√2/3) • (x - 1, y - 2)
z - 1 = (0, 3) • (x - 1, y - 2) / (√2/3)
Можно домножить на √2:
√2(z - 1) = 2 • (0, 3) • (x - 1, y - 2) / (√2/3)
Упростим:
√2(z - 1) = 6/(√2/3) • (x - 1, y - 2)
√2(z - 1) = 6/(√2/3) • (x - 1, y - 2)
√2(z - 1) = 6 • √3/√2 • (x - 1, y - 2)
√2(z - 1) = 3√3 • (x - 1, y - 2)
Таким образом, уравнение дотичной плоскости к поверхности z(x,y) в точке M(1,2) имеет вид:
√2(z - 1) = 3√3 • (x - 1, y - 2)
А уравнение нормали будет:
(x - 1, y - 2) = (1/9, 1/3) • (z - 1)