1. Математика
  2. (Log1/5((корень (х+3)^2)

(Log1/5((корень (х+3)^2) +(корень в 4 степени (2-х)4)) больше или равно -1 Найти количество целых решений неравенства

keke717 keke717    3   16.07.2021 12:45    1

Ответы
mgarkanov mgarkanov  15.08.2021 13:40
Решение:

    \log_{\frac{1}{5}} \Big( \sqrt{ (x+3)^2 } + \sqrt[4]{(2-x)^4} \Big )\geq -1

Так как степени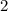 2 и 4 четные, нужно обязательно поставить модуль при упрощении подлогарифмического выражения:

    \log_{\frac{1}{5}} \Big( \Big | x + 3\Big | + \Big | 2-x\Big | \Big)\geq -1

Представим -1 как логарифм:

    \log_{\frac{1}{5}} \Big( \Big | x + 3\Big | + \Big | 2-x\Big | \Big)\geq \log_{\frac{1}{5}}5

Так как \frac{1}{5} < 1, знак неравенства меняется:

    \Big | x + 3\Big | + \Big | 2-x\Big | \leq 5

Полученное неравенство можно решить, например, методом интервалов:

1) x \leq -3

(-x-3)+(2-x) \leq 5 \\x \geq -3

  Здесь x =-3.

2) -3

(x+3)+(2-x) \leq 5 \\5 \leq 5

  Это правда: x \in (-3;2).

3) x \geq 2

(x+3)+(-2+x) \leq 5\\x \leq 2

  То есть x=2.

Собирая все воедино, получаем, что x \in \Big [-3;2 \Big ].

Целые решения: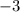 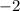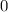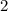-3, -2, -1, 0, 1, 2. Всего 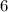6. Задача решена!

ответ: 6.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
КучеренкоИнна КучеренкоИнна  05.02.2022 03:25
На втором участке кустов малины в 3 раза больше, чем на первом. Когда на первый посадили 20 кустов, а на второй 10 кустов, то на втором участке кустов малины стало...
Urinasonya Urinasonya  05.02.2022 03:24
5×(х+3) = 6 × (х-3)ПОМГИИТЕЕЕ...
Котенька0209 Котенька0209  05.02.2022 03:19
15 л яблочного сока составляют одну часть из трёх.Сколько всего л сока?...
uztstdgiDima uztstdgiDima  05.02.2022 03:10
1. Реши буквенные выражения.а: 900, гдеa = 361800a = 51300a = 59400...
fedos1488 fedos1488  05.02.2022 03:09
СТОЛБИКОМ И ФОТО вычисли и выполни проверку 100000- 895 325864+546879 306400•503 968•547 3952:52 33855:111...
MaksimVip12 MaksimVip12  05.02.2022 03:05
1 1 из 8 Какие цифры можно поставить вместо * ,чтобы образовалось верное неравенство? 1,055 1,0*6 Запиши все возможние варианты, перечисляя цифры без запятой, например:...
Nika1032 Nika1032  05.02.2022 03:04
Обчисли раціональним : а)-2,5*(-0,52)*4 б)7,1*(-3/4)*1/1/3...
saida1808 saida1808  05.02.2022 03:03
2(4-9d) -(2d+3) =-8(4-d) +3(1+2d)...
ryckovan3 ryckovan3  02.04.2021 11:32
Прямая пропорциональность задана формулой y= 5/6x при каком значени x значение y=3,5​...
girb13 girb13  02.04.2021 11:32
Знайти значення виразу(√13−√12) ∕ (√13+√12) + (√13+√12) ∕ (√13−√12)​...

Популярные вопросы