1. Математика
  2. Lim (sinx*sin3x)/x^2

Lim (sinx*sin3x)/x^2 > 0 ответ 3 это первый замечательный предел

bmwm3gtr75 bmwm3gtr75    2   09.09.2019 23:20    1

Ответы
Shmanin32 Shmanin32  07.10.2020 04:11
Неопределённость 0/0 приводим к первому замечательному пределу. Икс в квадрате представляем как произведение иксов, которые относим к каждому из синусов. Во втором отношении доводим до первого замечательного предела путём умножения числителя и знаменателя на три.

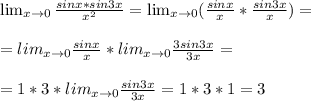
\lim_{x \to \inft0} \frac{sinx*sin3x}{x^2} = \lim_{x \to \inft0} (\frac{sinx}{x} *\frac{sin3x}{x}) = \\ \\ =lim_{x \to \inft0} \frac{sinx}{x} * lim_{x \to \inft0} \frac{3sin3x}{3x} = \\ \\ =1*3* lim_{x \to \inft0} \frac{sin3x}{3x}=1*3*1=3
ПОКАЗАТЬ ОТВЕТЫ
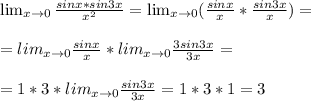
Другие вопросы по теме Математика
sashabulaev21 sashabulaev21  15.04.2020 14:20
Является ли пара чисел на х=1,5 и у=2 решением уравнения 2х-5у=7?почему? привидите ещё два примера решения этого уравнения​...
Rif05623 Rif05623  15.04.2020 14:20
Собственная скорость лодки 15 кмв час за 2 часа по течению реки она такоеже расстояние как за 3 часа против течения найдите скорость течения реки решение и уравнение и краткая запись...
zaharovvlad1337 zaharovvlad1337  15.04.2020 14:20
до шести часов. УМАЛАЮ 1.Балалар 10кг емен, қарағай және жөке дәндерін жинады. Барлық жиналған дәннің 60%-ын емен жаңғағы, 25%-ын қарағай дәні құрайды. Қанша килограмм жөке дәні жиналған?...
aishaefendieva aishaefendieva  15.04.2020 14:20
В книге 300 страниц.В 1 день мальчик прочитал 26% , во 2 день 34% .Сколько страниц осталось прочитать?​...
сонька2005бедовая сонька2005бедовая  15.04.2020 14:20
. Решите уравнения, предварительно раскрыв скобки 1. 12 + (x – 4 ) = 56 2. 85 – (– 18 – y) = 76 3. –906 – (36 + k) = – 120...
nesuk07 nesuk07  15.04.2020 14:20
А) - 3,8• 2,06 б) 25,641:5,3 в)-1,88:0,04 № 2Реши рациональным Вася потратил 82 рубля, что составило 40% имеющихся денег. Сколько денег осталось. № 4. Проехали 65% длины маршрута,...
tt9692069 tt9692069  15.04.2020 14:20
Решить ребус рыба+рыба= акула решить...
hudia4 hudia4  15.04.2020 14:20
В палатку привезли 5 ящиков огурцов по 12 кг в каждом. Через час четвёртую часть массы всех огурцов продали. Сколько килограммов огурцов осталось?...
Kristina122205 Kristina122205  15.04.2020 14:20
До ть будьласка то контрольна робота...
oleg1836 oleg1836  15.04.2020 14:20
Лист бумаги расчерчен на прямоугольники со сторонами 4 см и 6 см. 4 см 6 см 1) Нарисунке полиниям изображена фигура. Найдите площадь этой фигуры. ответ дайте в квадратных сантиметрах....

Популярные вопросы