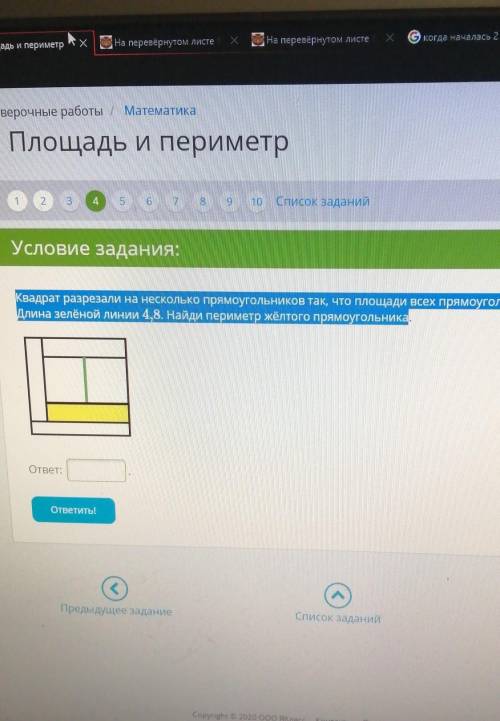
Квадрат разрезали на несколько прямоугольников так, что площади всех прямоугольников оказались равны. Длина зелёной линии 4.8. Найдите периметр жёлтого прямоугольника. ​

Для решения данной задачи, нам необходимо использовать свойство равности площадей прямоугольников, а также длину одной из сторон квадрата.

Итак, у нас дана длина зелёной линии, которую мы обозначим за "а". Заметим, что желтый прямоугольник является наименьшим из всех прямоугольников, которые были получены разрезанием квадрата. Пусть его длина будет равна "b", а его ширина - "с".

Так как площадь каждого прямоугольника должна быть одинаковой, мы можем записать следующее равенство:

a * a = b * c

Далее, мы знаем, что квадрат имеет все стороны одинаковой длины. Пусть длина стороны квадрата будет "d".

Тогда, по теореме Пифагора, мы можем выразить "a" через "d":

d * d = a * a + b * b

Отсюда выразим "b":

b = √(d * d - a * a)

Теперь, чтобы найти периметр желтого прямоугольника, нам нужно сложить все его стороны:

Периметр = 2 * (b + c)

Заменим значение "b" из предыдущего шага:

Периметр = 2 * (√(d * d - a * a) + c)

Теперь осталось выразить "c". Мы знаем, что площадь прямоугольника равна произведению его сторон. Поэтому, площадь желтого прямоугольника будет равна:

Площадь = b * c

Из первого равенства ("a * a = b * c"), мы можем выразить "c":

c = (a * a) / b

Заменим значение "b":

c = (a * a) / √(d * d - a * a)

Теперь мы знаем и "b", и "c", и можем подставить их в формулу для периметра:

Периметр = 2 * (√(d * d - a * a) + (a * a) / √(d * d - a * a))

Если полученная формула показалась сложной для понимания, то вы можете использовать значения, которые даются в задаче, и подставить их в формулу, чтобы найти периметр желтого прямоугольника.