Координаты точки M(x, y) удовлетворяют системе уравнений 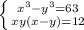 Найти сумму координат точки M. Если таких точек несколько, в ответ записать наименьшую сумму.
Найти сумму координат точки M. Если таких точек несколько, в ответ записать наименьшую сумму.
Популярные вопросы
- Решить 6й пример подробно и понятно...
3 - 1. Как звали дочку Бирюка из рассказа И.С. Тургенева «Бирюк»? 1) Алёна...
1 - 5.Найдите слово, в корне которого пропущена безударная проверяемая гласная....
3 - Каково значение названия пьесы вишневый сад ? Имеет ли оно прямое и символическое...
1 - Перед вами таблица плотностей некоторых жидкостей и твердых тел. Какое...
3 - Сочинение на тему Леонардо да Винчи как символ эпохи Возрождения....
2 - 1. Складним є речення (розділові знаки пропущено) А І хочеться знати куди...
1 - Определить элемент VII группы. Относительная молекулярная масса его летучей...
1 - Как сделать проверку титра раствора щелочи? И контрольный анализ кислоты?...
3 - Яку силу треба прикласти до важеля завдовжки 2 м, щоб підняти камінь масою...
3
-5
Пошаговое объяснение:
,,,,,,,,,,,,,,,,,,,,,,,,
-5
Пошаговое объяснение: