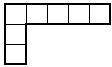
Клетчатый шестиугольник, составленный из двух полосок ширины 1, пересекающихся по одной клетке, назовём уголком. Докажите, что произвольный клетчатый квадрат без любой клетки можно разбить на клетчатые уголки с различным нечётным числом клеток. Сколько существует таких разбиений для квадрата 5×5 с вырезанной центральной клеткой?

Клетчатый шестиугольник, составленный из двух полосок ширины 1, пересекающихся по одной клетке, назо

Ответы

twinnyXD 16.12.2020 17:30

У нас 4^n-1 клеток. докажем, что 4^n-1 делится на 3

При n=1 4-1=3 - делится

Пусть при некотором n=k 4^k-1 делится на 3

докажем, что в этом случае 4^(k+1)-1 делится на 3

4^(k+1)-1=4×4^k-1=(3+1)×4^k-1=3×4^k+(4^k-1) первоеслагаемое кратно 3, второе делится на 3 по предположению, сл-но 4^(k+1)-1 делится на 3 для любого n

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика

sofiy12grazdovskava 07.04.2020 19:28

bambam4 07.04.2020 19:28

Толиk 07.04.2020 19:28

sbelikova44 07.04.2020 19:29

Sopfia3333333333333 07.04.2020 19:29

Розв яжи рівняння 64:(12-а)=8...

respons 07.04.2020 19:29

Реши уравнения. S - 0,375=0,73. T - 4,195=7,0005...

qweravq 07.04.2020 17:50

ЯРеши уравнение и выполни проверку x•8+20=36...

noer2000 07.04.2020 17:50

Найди последнюю цифру числа 3897...

irenda828001 18.12.2019 21:56

NargizzaErbolat 18.12.2019 21:56