Каз• Цилиндрдің радиусы 6 см , биіктігі 5 см . Цилиндрдің осіне параллель және табан шеңберінен 60 ° доғаны қиып түсіретін жазықтықпен қиғанда пайда болған қиманың ауданын табыңдар.
Рус•
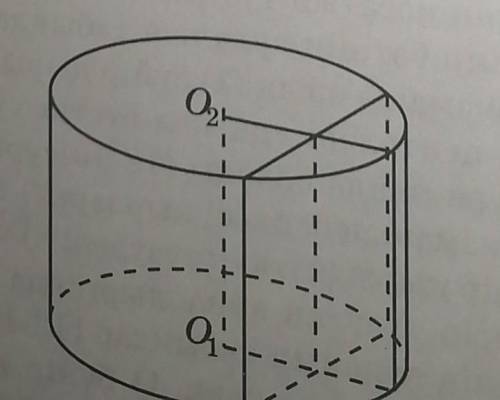
Цилиндр имеет радиус 6 см и высоту 5 см. Найдите площадь поперечного сечения, образованного путем вырезания дуги, параллельной оси цилиндра, и вырезания дуги 60 ° от окружности стопы.​

Для решения данной задачи нам понадобятся некоторые геометрические понятия и формулы.

Дано: радиус цилиндра (r) = 6 см, высота цилиндра (h) = 5 см, угол дуги (α) = 60 °.

Нам нужно найти площадь поперечного сечения, образованного вырезанием дуги из цилиндра. Для этого разобьем процесс на несколько шагов:

Шаг 1: Найдем длину дуги (часть окружности), образованной вырезанием дуги.
Длина дуги (L) можно найти, используя следующую формулу:
L = (α/360) * 2πr,
где α - угол дуги, r - радиус цилиндра, π - математическая константа, примерно равная 3.14.
В нашем случае:
L = (60/360) * 2 * 3.14 * 6.

Шаг 2: Найдем площадь сектора, образованного этой дугой.
Площадь сектора (A) можно найти, используя следующую формулу:
A = (α/360) * π * r^2,
где α - угол сектора, r - радиус цилиндра, π - математическая константа, примерно равная 3.14.
В нашем случае:
A = (60/360) * 3.14 * 6^2.

Шаг 3: Найдем площадь треугольника, образованного этой дугой и стороной цилиндра.
Площадь треугольника (B) можно найти, используя следующую формулу:
B = (1/2) * L * h,
где L - длина дуги, h - высота цилиндра.
В нашем случае:
B = (1/2) * L * 5.

Шаг 4: Найдем площадь поперечного сечения.
Для этого вычтем площадь треугольника из площади сектора:
S = A - B.

Теперь решим это пошагово:

Шаг 1: Найдем длину дуги.
L = (60/360) * 2 * 3.14 * 6,
L = (1/6) * 2 * 3.14 * 6,
L = 6.28 см.

Шаг 2: Найдем площадь сектора.
A = (60/360) * 3.14 * 6^2,
A = (1/6) * 3.14 * 36,
A = 18.84 см^2.

Шаг 3: Найдем площадь треугольника.
B = (1/2) * L * 5,
B = (1/2) * 6.28 * 5,
B = 15.7 см^2.

Шаг 4: Найдем площадь поперечного сечения.
S = A - B,
S = 18.84 - 15.7,
S = 3.14 см^2.

Таким образом, площадь поперечного сечения, образованного вырезанием дуги из цилиндра, равна 3.14 см^2.