Какие значения НЕ может принимать ордината точки на единичной полуокружности, расположенной в первом и втором квадрантах? 1
-1
0
0,009
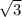
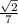
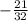
Другие вопросы по теме Математика
Популярные вопросы
- Как определить степень окисления всех элементов в следующей формуле: fe2o3+3co=2fe+3co2...
3 - Рассчитайте массу воды и сахара необходимые для приготовления 140 г 14...
2 - Через какой орган организма удаляются пары воды , газы ....
3 - Огамский алфавит с переводом на подскажите...
3 - Всем ! решите тест по языку. 30 . 1)укажите слово в котором больше звуков...
1 - Вмагазине продали за день 265 кг сахарного песка. после этого в магазине...
1 - Найдите площадь треугольника со сторонами 9, 8 и 4 см....
3 - Решить: номер 847: округлите: до десятков: 534; 18357; 4783 386; до сотен:...
1 - А)сформируй на движение в одном направлении ,используя следующую схему...
3 - На одному тракторі працювали протягом тиждня 60годин а на другому тиждні...
2
Единичная полуокружность представляет собой полуокружность радиусом 1, расположенную в декартовой системе координат. Она делит плоскость на два квадранта: первый квадрант (I), где x>0 и y>0, и второй квадрант (II), где x<0 и y>0.
На полуокружности, ордината точки представляет собой y-координату этой точки. Так как полуокружность находится на расстоянии 1 от начала координат, значит всякий раз, когда мы находимся на этой полуокружности, значение ординаты точки y будет равно 1 или -1.
Исходя из приведенной задачи, имеем следующие варианты ответа:
1) 1 - Это значение может принимать ордината точки на единичной полуокружности, ведь она лежит на полуокружности на расстоянии 1 от начала координат.
2) -1 - Это значение также может принимать ордината точки на единичной полуокружности, так как она также лежит на полуокружности на расстоянии 1 от начала координат.
3) √3 - Данное значение не может принимать ордината точки на единичной полуокружности, так как оно превышает размерность полуокружности. Максимальное значение ординаты на полуокружности равно 1, а √3 больше единицы. Таким образом, ответ: НЕ может принимать значение √3.
4) 0 - Данное значение также не может быть ординатой точки на единичной полуокружности. Все точки на полуокружности находятся над осью абсцисс и имеют положительную ординату, поэтому значение 0 противоречит определению полуокружности. Таким образом, ответ: НЕ может принимать значение 0.
5) 0,009 - Это значение может принимать ордината точки на единичной полуокружности, если ордината этой точки находится на полуокружности на расстоянии 0,009 от начала координат. Поскольку полуокружность находится на расстоянии 1 от начала координат, значение 0,009 вполне допустимо для ординаты точки на полуокружности.
6) √2/7 - Данное значение не может быть ординатой точки на единичной полуокружности. Это значение является дробной и меньше 1, поэтому не может быть равным 1 или -1, что является допустимыми значениями ординаты на полуокружности. Таким образом, ответ: НЕ может принимать значение √2/7.
7) -21/32 - Данное значение также может принимать ордината точки на единичной полуокружности, если она находится на полуокружности на расстоянии -21/32 от начала координат. Здесь "-" обозначает отрицательное значение, а 21/32 - относительное расстояние. Таким образом, значение -21/32 вполне допустимо для ординаты точки на полуокружности.
Итак, ответ на данный вопрос: НЕ может принимать значения √3 и √2/7.
Я надеюсь, что объяснение было понятным и подробным. Если у тебя возникнут еще вопросы или что-то будет не ясно, пожалуйста, сообщи мне!