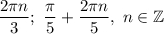Какие углы х можно увеличить в 4 раза так, что их синусы окажутся равными?
Другие вопросы по теме Математика
Популярные вопросы
- Сколько процентов азота содержится в nh4no3...
1 - Решить уровнения в столбик 4 класс 238: 7,474: 6,783: 9,165: 5....
3 - Напишите 4 сложно сочинённых предложения и 4 сложно подчинённые предложения...
1 - Напишите рассказ об осени из пяти шести предложений, используя данные слова.(можно...
1 - Точка m(16; -64 принадлежит графику функции y=kx.принадлежит ли графику этой...
1 - Отрицательные и положительные персонажи в произведение недоросль...
1 - Значение фразеологизма кот наплакал раз два и обчелся дохнуть (дыхнуть) негде...
1 - Найди существительные которые называют одни и те же предметы. в ташкенте...
3 - Надо дать характеристики героя- садко...
2 - 6класс длина большого алматиского канала приближенно равно 170 км а на карте...
3
После увеличения угла в 4 раза мы получим угол
в 4 раза мы получим угол 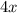 . По условию их синусы равны. Составляем уравнение:
. По условию их синусы равны. Составляем уравнение:
Произведение равно нулю, когда один из множителей равен нулю. Поэтому уравнение распадается на два:
ответ: