Как решить данное дифференциальное уравнение? Я так полагаю, это диф. уравнение второго порядка без искомого y, допускающее понижение порядка? Пытался решить заменой y" на p*p' и y' на p - не выходит.
.

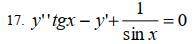
Как решить данное дифференциальное уравнение? Я так полагаю, это диф. уравнение второго порядка без

Ответы

iroytblatилья 10.05.2021 20:14

$y''tg(x) - y'= - \frac{1}{ \sin(x) } \\$

Замена:

$y'= p (x)\\ y'' = p'(x)$

$p'tg(x) - p = - \frac{1}{ \sin(x) } \\ | \div tg(x) \\ p' - \frac{p}{tgx} = - \frac{1}{ \sin(x) tgx} \\ p' - pctgx = - \frac{ctgx}{ \sin(x) } \\ \\ p = uv \\ p' = u'v + v'u \\ \\ u'v + v'u - uvctgx = - \frac{ctgx}{ \sin(x) } \\ u'v + u(v' - vctgx) = - \frac{ctgx}{ \sin(x) } \\ \\ 1)v' - vctgx = 0 \\ \frac{dv}{dx} = vctgx \\ \int\limits \frac{dv}{v} = \int\limits \frac{ \cos(x) }{ \sin(x) } dx \\ ln |v| = \int\limits \frac{d (\sin(x)) }{ \sin(x) } \\ ln |v| = ln | \sin(x) | \\ v = \sin(x) \\ \\ 2)u'v = - \frac{ctgx}{ \sin(x) } \\ \frac{du}{dx} \times \sin( x ) = - \frac{ctgx}{ \sin(x) } \\ \int\limits \: du = \int\limits \: ctgx \times ( - \frac{1}{ \sin {}^{2} (x) } )dx \\ u = \int\limits \: ctgx \: d(ctgx) = \frac{ctg {}^{2}x }{2} + C_1 \\ \\ p = uv = \\ = \sin(x) \times ( \frac{ {ctg}^{2}x }{2} + C_1) = \\ = \frac{ \sin(x) {ctg}^{2}x }{2} + C_1 \sin(x) \\ \\ y = \int\limits(\frac{ \sin(x) {ctg}^{2}x }{2} + C_1 \sin(x)) dx \\$

$1) \frac{1}{2} \int\limits \sin(x) \times \frac{ \cos {}^{2} (x) }{ \sin {}^{2} (x) } dx = \frac{1}{2} \int\limits \frac{ \cos {}^{2} (x) }{ \sin(x) } dx = \\ = \frac{1}{2} \int\limits \frac{1 - \sin { }^{2} (x) }{ \sin(x) } dx = \frac{1}{2} \int\limits( \frac{1}{ \sin(x) } - \sin(x)) dx = \\ = \frac{1}{2} ( ln( |tg \frac{x}{2} | ) + \cos(x) + C_2) = \\ = \frac{1}{2} ln( |tg \frac{x}{2} | ) + \frac{1}{2} \cos(x) + C_2 \\ \\ 2)\int\limits \: C_1 \sin(x) dx = - C_1 \cos(x) + C_2 \\ \\ y = \frac{1}{2} ln( |tg \frac{x}{2} | ) + \frac{1}{2} \cos(x ) - C_1 \cos(x) + C_2 = \\ = \frac{1}{2} ln( |tg \frac{x}{2} | ) + ( \frac{1}{2 } - C_1) \cos(x) + C_2 = \\ = \frac{1}{2} ln( |tg \frac{x}{2} | ) - C_1 \cos(x) + C_2$