1. Математика
  2. Как перемножать логарифмы с

Как перемножать логарифмы с одинаковыми основаниями? нужно подробное решение этого:

radchenkoalink radchenkoalink    1   23.12.2019 14:04    1

Ответы
KlodMone1 KlodMone1  10.10.2020 22:41

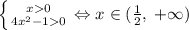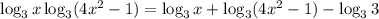Необходимым условием для существования решение является \left \{ {{x0} \atop {4x^2-10}} \right.\Leftrightarrow x\in\((\frac{1}{2},\;+\infty); Теперь можно преобразовать: \log_{3}x\log_{3}(4x^2-1)=\log_{3}x+\log_{3}(4x^2-1)-\log_{3}3;

(\log_{3}(4x^2-1))(\log_{3}x-1)=\log_{3}x-1\Leftrightarrow (\log_{3}x-1)(\log_{3}(4x^2-1)-1)=0; Отсюда легко найти корни: \textbf x=3,\; \log_{3}(4x^2-1)=1 \Rightarrow 4x^2-1=3 \Leftrightarrow \textbf x=\pm 1; Удовлетворяют найденному в начале промежутку лишь два корня - 1 и 3.

                                                                                     ответ: 1; 3

Рассмотрим отрезок [\log_{5}2,\; \log_{5}27]; Теперь отвлечемся. Пусть дан отрезок [a,\; b]; Если x_{0}\in[a,\;b] \Leftrightarrow 5^{x_{0}}\in[5^{a},\;5^{b}]; Для нашего отрезка: 5^{x_0}\in[2,\;27]; Очевидно, что 3 не входит (5*5*5=125), но 1 подходит.

                                                                                    ответ: 1.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
zaj2015 zaj2015  01.06.2019 14:20
1)напишите три правильные и две неправильные дроби, для каждой из которых сумма числителя и знаменателя равна 18 2)по учащиеся должны собрать 480 кг семян дуба. было...
ksenia231106 ksenia231106  01.06.2019 14:20
Грузовая машина при перевозке мебелиизрасходывала до остановки 48 литров горючего а послеостановки 32 литра сколько часовбыла в пути машина если за 1 час расходывалось...
GreenBaguette GreenBaguette  01.06.2019 14:20
Реши по действиям в двух пачках 270 тетрадей. сколько тетрадей в каждой пачке, если в одной из них тетрадей в 4 раза меньше, чем в другой? при затруднее подумай над...
gallagersandr gallagersandr  01.06.2019 14:20
А) 71,7*9,010= б)2,3456789*0,3= в) 21,004*6,5= г) 45,34*20,01=...
14ксенечка15 14ксенечка15  01.06.2019 14:20
Подумай гормонично ли музыкальное произведение звучащие исключительно в мажоре .содержашие только благозвучие заранее )...
IrishkaKoteika2689 IrishkaKoteika2689  01.06.2019 14:20
Округлите до десятых 6,7489 округлите до сотых 3,61502...
Baby1FNAF Baby1FNAF  01.06.2019 14:20
Впервых классах школы учится 150 , а в десятых 75. во сколько раз числопервоклассников больше числа десятиклассников? на сколько процентов числопервоклассников больше...
Маруська246 Маруська246  01.06.2019 14:20
Знайти половину числа 16,тритину числа 15,чверть числа 24,і третину числа 24...
zlpa zlpa  01.06.2019 14:20
Поночка выризала 12 маленьких снежинок.она розлажила их поровну в 3 кортонние коробки.сколько снежинок в каждой значений вирожений 3*а-7,если а=4,а=8.в недели 5 рабочих...
maxmxax25245 maxmxax25245  01.06.2019 14:20
Выполните сложение -43+75= 37+(-56)= 3,10+(4,5)= 4,61+(-2.29)= -3.08+1.69= -9. 5,6+2. 3,4...

Популярные вопросы