Как найти множество значений функции? объясните
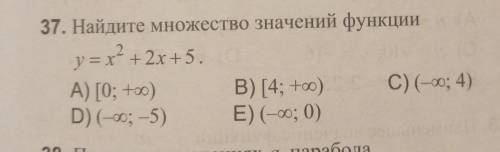
Другие вопросы по теме Математика
Популярные вопросы
- Найдите наибольшее и наименьшеезначения функции y=x? на заданномпромежутке:все...
1 - 2.17 Listen to the key phrases 1-4 and replywith the correct responses a-d. Then...
2 - Решите задания по теме Неметаллы очень...
3 - История 10 класс, в вк скину полный параграф...
1 - Чат ашу - 1dcc2тапсырмаларды орындау. Кітаппен жұмыс. 108-бет. Білу бөлімі1. Жазу...
3 - Для правильноговимірювання температуриповітря вимірювальнийХприлад встановлюють...
2 - Фото сверху дам- 5-тапсырма. Берілген етістіктерге өздік етіс жұрнағын жалғап,сөйлем...
3 - Политическая внешняя среда косвенного воздействия предприятия включает в себя:...
2 - Прочитайте текст, относящийся к периоду правления Ивана IV. Назовите исторического...
3 - Висловіть власну думку щодо українського питання в контексті європейської політики...
2
E(y)=[4,+∞)
Пошаговое объяснение:
y=x^2+2*x+5- это квадратичная функция, графиком является парабола.
Коэффициент при x^2 равен 1, т.е. a=1>0, значит, ветви параболы направлены вверх.
Найдем координаты вершины параболы:
х0=(-b)/(2*a)
x0=(-2)/(2*1)= -2/2= -1 Подставим значение х в функцию:
y0=(-1)^2+2*(-1)+5=1-2+5=4
Тогда множество значений у от у0 до бесконечности
E(y)=[4,+∞)