Известно, что мы можем представить любое квадратное уравнение  в виде
в виде  , где x1 и x2 — это корни исходного уравнения. Что происходит в уравнении
, где x1 и x2 — это корни исходного уравнения. Что происходит в уравнении 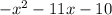 ? Его корни — это -1 и -10. Но когда мы представляем это уравнение через корни, мы получаем
? Его корни — это -1 и -10. Но когда мы представляем это уравнение через корни, мы получаем  , а
, а 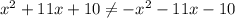 .
.
Подскажите , почему так получилось. Заранее благодарю за .
Другие вопросы по теме Математика
Популярные вопросы
- Ширина меньше длины в 3 раза, найти пер метр если ширина 40 см в...
1 - Найдите значение выражения 3a-2b при a=1/4 и b =-1...
2 - А) напишите уравнение реакции с которых можно осуществить превращения:...
1 - Сколько стоят бисквитные коржики в магните? скажите , надоо; )...
2 - 7деталей одинак. веса, а 1 деталь из лёгкого сплава , надо узнать...
1 - Вариант 6 1. количество теплоты, выделившееся при полном сгорании...
2 - Доклад на тему портрет половцев ....
2 - Когда с газом вынесли из комнаты на улицу,давление в упало на 10%....
2 - Сколько слагаемых под корнем в равенстве√7^2+7^2++7^2=7^2+7^2+7^2...
3 - Построить в соль миноре тритоны ув2 уч7 d7 с обращениями 35 за лучший...
1
Так получается, потому что изначально условие записано не верно.
Пошаговое объяснение:
То есть, в условии написано "уравнение", однако представлено не уравнение, а лишь квадратный трехчлен, нет знака =
Если бы он был, то в конце получилось бы не неверное равенство, а два уравнения, которые были бы равносильны(т.е.имели одинаковые корни), так что никакого противоречия и не возникло бы.