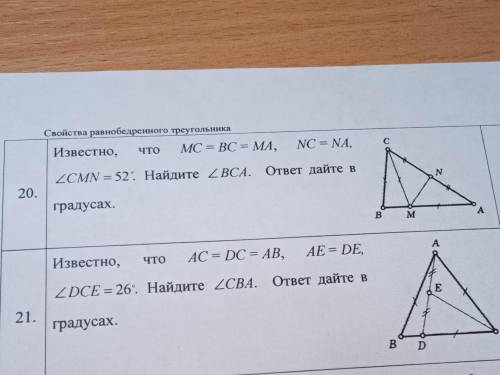
Известно, что MC = BC = MA, NC = NA, УголCMN = 52". Найдите уголBCA. ответ дайте в градусах.

Номер 20

Для решения данной задачи, нам нужно использовать свойство равнобедренных треугольников, а именно: в равнобедренном треугольнике боковые стороны и прилежащий к ним угол равны.

Исходя из известных данных в задаче, у нас имеется треугольник ACN, в котором сторона AC, равна стороне NC (так как NC = NA), и угол ACM равен углу CMN (так как MC = MA). Таким образом, в треугольнике ACN имеются два равных угла, ACM и CMN.

Поскольку сумма всех углов треугольника равна 180 градусов, мы можем выразить угол ACN через равные углы ACM и CMN:

Угол ACN = 180 - (угол ACM + угол CMN)

Подставим вместо угла ACM и угла CMN известные значения:

Угол ACN = 180 - (угол ACM + 52)

Следовательно:

Угол ACN = 180 - (2 * ACM) - 52

Следующим шагом нам нужно найти значение угла ACM. Мы можем использовать свойство треугольника, согласно которому сумма всех углов в треугольнике равна 180 градусов. В треугольнике ABC имеется угол BCA, и так как углы BCA и BCM являются смежными, их сумма равна 180 градусов:

Угол ACM = 180 - угол BCA

Теперь мы можем вернуться к нашему первоначальному уравнению и заменить ACM на выражение 180 - угол BCA:

Угол ACN = 180 - (2 * (180 - угол BCA)) - 52

Упростим это уравнение:

Угол ACN = 180 - (360 - 2 * угол BCA) - 52

Угол ACN = 180 - 360 + 2 * угол BCA - 52

Угол ACN = -180 + 2 * угол BCA - 52

Теперь у нас есть уравнение, которое позволяет нам найти значение угла BCA.

Если мы добавим 180 к обоим сторонам уравнения, то получим:

180 + угол ACN = 2 * угол BCA

(180 + угол ACN)/2 = угол BCA

Так как угол BCA — это то, что мы хотим найти, мы можем выразить его через другие известные углы и стороны в треугольнике.

Таким образом, ответом на задачу будет:

Угол BCA = (180 + угол ACN)/2

Чтобы получить численное значение угла BCA, нам нужно знать значение угла ACN. Однако данная информация не предоставлена в условии задачи. Если она будет предоставлена, мы сможем рассчитать значение угла BCA.