Из колодыиз 36карт 10разизвлекаютпо одной картеи кладуткарту обратнов колодуперед следующимиспытанием.какова вероятность того,что среди 10вытянутыхкарт будуттри туза

Ответы

kozaksolomia1 12.06.2020 00:25

Всего исходов $36^{10}$ , так как карты возвращают в колоду.

Положительных исходов: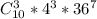 $C^{3}_{10}*4^3*36^7$

$C^{3}_{10} = 120$

p(вытащить три туза) =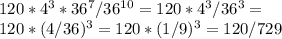 $120*4^3*36^7/ 36^{10} = 120*4^3/36^3 = \\ 120*(4/36)^3 = 120*(1/9)^3 =120/ 729$

ПОКАЗАТЬ ОТВЕТЫ

matvey9874 12.06.2020 00:25

Это пример схемы Бернулли, так как тут мы рассматриваем независимые повторения(независимые, потому что мы каждый раз возвращаем вытянутую карту обратно в колоду и следовательно вероятность вытянуть туз не меняется, она равна 4/36) одного и того же испытания с двумя исходами (либо туз либо любая другая карта), которые условно можно назвать “успех”(если вытянули туз) и “неудача”( если вытянули любую другую карту).

Значит мы можем применить теорему Бернулли, чтобы решить эту задачу. Теорема Бернулли гласит, что вероятность наступления “k” успехов в “n” независимых повторениях одного и того же испытания находится по формуле P=C(k,n)*(p^k)*(q^(n-k)), где C(k,n)=число сочетаний “k” по “n”, p=вероятность “успеха”, q=вероятность “неудачи”=1-p.

Значит вероятность того, что среди 10 вытянутых карт будут три туза равна:

P=120*((4/36)^3)*((32/36)^7)=приблизительно 0.072175

ответ: Вероятность того, что среди 10 вытянутых карт будут три туза приблизительно 0.072175

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика