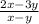Из 2–х пакетов молока разной жирности весом 4кг и 6кг отлили одинаковое количество молока. то что отлили из первого ,смешали с остатками второго пакета,а то что отлили из второго пакета смешали с остатками первого пакета. в обоих пакетах жирность стала одинаковой. сколько отлили молока?
Другие вопросы по теме Математика
Популярные вопросы
- Новоторовый уставВсероссийский рынокКазачествоЧерноcошные крестьянеБоярская думаЗемские...
3 - осталось очень мало времени задание на фото...
3 - Против теяения 1,4 ч если что...
2 - 2. При открытом парашюте парашютист равномерно спустился с высоты 412 м в течение...
2 - Писать только так: 1-ж На предложениями...
3 - Составьте пищевую цепь: щука планктон, плотва...
1 - Сократите дроби надо сократить...
3 - Выполните на листочке задания...
3 - 785,13,32,630 нужно эти чеслительные перевести в топтау сан есім....
1 - 1.Заполните таблицу.(вставить слова) Голосеменные имеют| У голосеменных отсутствуют...
2
ответ: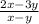
Пошаговое объяснение:
Пусть в первом пакете, весом 4кг, будет x % жирности, или же 0,01x
Пусть во втором пакете, весом 6 кг, будет y % жирности, или же 0,01y
Пусть из двух пакетов отлили одинаковое кол-во молока - k кг
1) После того, как из первого пакета отлили k кг молока, в нём осталось
4 - k кг молока;
значит масса жира первого пакета стала 0,01x·(4 - k) кг
2) После того, как из второго пакета отлили k кг молока, в нём осталось
6 - k кг молока;
значит масса жира второго пакета стала 0,01y·(6 - k) кг
3) В первый пакет добавили k кг молока из второго пакета, с массой жира 0,01y·k
Значит масса жира в первом пакете стала
0,01x·(4 - k) + 0,01y·k кг
Во второй пакет добавили k кг молока из первого пакета, с массой жира 0,01x·k
Значит масса жира во втором пакете стала
0,01y·(6 - k) + 0,01x·k кг
4) По условию жирность в двух пакетах стала одинаковой, значит можем составить уравнение:
0,01x·(4 - k) + 0,01y·k = 0,01y·(6 - k) + 0,01x·k | ×100
4x - xk + yk = 6y - yk + xk
4x - 6y = 2xk - 2yk
2x - 3y = k(x - y)
k =