Исследуйте на сходимость ряд:
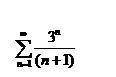
Другие вопросы по теме Математика
Популярные вопросы
- Почему на езде автомобиля необходимо пристегнуть...
3 - Сравните дробь 1) 9/10 и 4/5 2) 4/7 2/3...
2 - Определите и запишите основную мысль текста. прочитайте текст 2...
3 - Частота вращения тела при равномерном движении по окружности радиусом...
1 - На соревнования по настольному теннису учавствовали равные по составу...
1 - Найти основную мысль текста. составить тезисный план. ранним утром,...
1 - Данаарифметическая прогрессия мумма первыхее 10членов оавна 60а...
2 - Примеры эффективного и неэффективного использования ресурсов в твоей...
3 - Объясните термины коалиция контрибуция континентальная блокада заранее...
3 - Внаборе были гирьки массой 5, 24 и 43 грамма, поровну каждого вида....
2
ответ: ряд расходится.
Пошаговое объяснение:
1) Составляем выражение для n+1 - го члена: a(n+1)=3^(n+1)/(n+2)=3*3^n/(n+2).
2) Составляем отношение n+1 - го члена к n - му: a(n+1)/a(n)=3*(n+1)/(n+2).
3) Находим предел этого отношения при n⇒∞: он равен 3>1, поэтому по признаку Даламбера ряд расходится.
Вообще говоря, здесь можно обойтись и без признака Даламбера. Так как при любом n 3^n>n+1, то a(n) при n⇒∞ не стремится к нулю, а это достаточный признак расходимости ряда.