Исследуйте функцию f(x)=lg(x+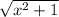 ) на четность/нечетность
) на четность/нечетность
Другие вопросы по теме Математика
Популярные вопросы
- Почему при ожогах щелочами поврежденное место необходимо обильно промывать водой?...
2 - Нужно выписать из любой сказки из любого рассказа 2 распространённых и 2 нераспространённых...
3 - Реши . ребро куба равно 7 см. найдите площадь поверхности и объем куба вас...
2 - 57 кг яблок разложили в 5 больших корзин и 3 маленькие корзины. сколько килограммов...
1 - Надо! решите что можете)заранее 1. выражение ctg(2п+a)*sin(п\2+a) cos(п-a)*tg(3п\2-a)...
2 - Составьте уравнение реакций по следующим данным: при окислении алюминия кислородом...
2 - Что отличает мораль лт других видов социальных норм? это рабочая тетради за...
2 - Написать изложение, применяя исключение, обобщение, , замену (не менее 70 слов)....
2 - 2. какие пары ионов могут одновременно находиться в растворе : а) cu2+ и он--;...
2 - Мне задали презентация и сообщение на тему прямокрылые кузнечики...
3
Нечетная.