Исследуйте функцию f(x)=8x^2-x^4-7 !
Другие вопросы по теме Математика
Популярные вопросы
- Какой ответ на этот ребус один+один=...
2 - Широко расстилались, луга осыпанные цветами. словосочетания и синтаксически...
2 - Спишите текст, вставляя орфограммы и недостающие знаки препинания. заполните...
2 - Переведите: write a similar story about your father or about your mother...
3 - Какие животные принадлежат к типам 1.суккуленты 2.эксерофиты 3.стипаксерофиты...
2 - Примеры растений-паразитов и отдельно примеры растений-полупаразитов...
3 - Никто не имеет права удерживать вас в рабстве,потому что? напишите типа как...
2 - Скакой скоростью брусок равномерно поднят на высоту 1,5 м, если время подъёма...
3 - Образовать страдательные причастия настоящего времени от глаголов: проверять,...
2 - Сколько слов читают учёные? за 1 мин сама мне не верит что я прочитала 402...
3
Исследовать функцию и построить график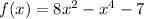
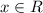
 точка пересечение (0; -7)
точка пересечение (0; -7)
1) Область определения функции. Функция определена на всей числовой оси, то есть
2) Точки пересечения графика функции с осью OY
Тоски пересечения с осью ОХ, т.е. у=0, тогда
Пусть x² = t, тогда
Корни квадратного уравнения t=1 и t=7
Сделаем обратную замену
Получили еще четыре точки
3) Исследуем функции на четность
Так как , то функция является четной
, то функция является четной
4) Функция не имеет точек разрыва, поэтому график не имеет вертикальных асимптот.
Найдем наклонные асимптоты , где
, где
Наклонных асимптот тоже нет.
5) Найдем экстремумы функции. Для это найдем производную y' и приравняем ее к нулю y' = 0
Тогда
Получились три критические точки.
Эти точки разбивают область определения на четыре интервала. Находим знак производной f'(x) в каждом из интервалов
На первом x < -2 , f'(x) > 0 - функция возрастает
На первом -2 < x < 0 , f'(x) < 0 - функция убывает
На первом 0 < x < 2 , f'(x) > 0 - функция возрастает
На первом x > 2 , f'(x) > 0 - функция убывает
Таким образом в при х=-2 и х = 2 - тока максимума,
а при х = 0 - тока минимума.