1. Математика
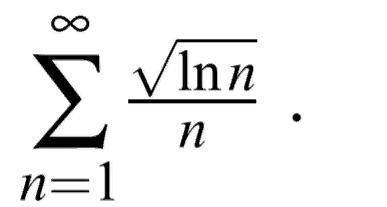
  2. Исследовать сходимость ряда

Исследовать сходимость ряда


Исследовать сходимость ряда

tima23qwerty tima23qwerty    3   19.06.2021 14:00    3

Ответы
ksenyarobulet ksenyarobulet  19.07.2021 14:58

Проверим ряд на необходимый признак сходимости:

\displaystyle \lim_{n \to \infty} a_n =0 \\\\ \lim_{n \to \infty} \frac{\sqrt{ln(n)}}{n} = \frac{\infty}{\infty}

Врятли преобразование приведёт к каким-то улучшениям, используем метод Лопиталя:

\displaystyle \lim_{n \to \infty} \frac{1}{2n\sqrt{ln(n)}} =\bigg[\frac{1}{\infty} \bigg]=0  - ряд может как сходиться, так и расходиться.

стоит отметить, что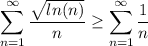  \displaystyle\sum^\infty_{n=1}\frac{\sqrt{ln(n)} }{n}\geq \sum^\infty_{n=1}\frac{1 }{n}

начиная с n = 3

\displaystyle e\approx2.72 , \quad \quad ln(3) \approx 1.04 , \quad\quad \frac{\sqrt{1.04}}{3} \frac{1}{3}

по-этому, исходный ряд расходится, по предельному признаку сравнения.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Politik2000 Politik2000  20.05.2020 11:55
{2х + 5у = 11 х-у = 1 { х+у=7 2х -у...
vovan2002vovap0181f vovan2002vovap0181f  20.05.2020 11:55
Решите эти уравнения X+43=4*2+50 327-20*x=267 (450:x+50):70=2...
calusiker calusiker  20.05.2020 11:55
Математикадан көмектесіңдер...
Prinsess1 Prinsess1  20.05.2020 11:55
На рисунке приведён график движения пешеходов в течение 3 часов .Чему равна средняя скорость пешехода с 14.00 до 16.00​...
anton12535 anton12535  20.05.2020 11:55
Произведение суммы и разности чисел 2 и 3/4...
liza345789 liza345789  20.05.2020 11:55
178 умножить на 9719827173298...
lolisgd lolisgd  20.05.2020 11:55
Одна из точек, отмеченных на координатной прямой, соответствует числу 53 Какая это точка контрольная по алгебре 8 класс....
Элиза5511 Элиза5511  20.05.2020 11:55
49,6-2 3/4•(1 9/11x+12/55)=-4 1/7•(21/29x+1 6/29)...
Meowwwwwwwwwwwwwwwww Meowwwwwwwwwwwwwwwww  20.05.2020 11:55
10 клас) буду очень благодана☺​...
камаз9 камаз9  20.05.2020 11:55
Отношение двух чисел равно 57Вычисли эти положительные числа, если их разность равна 0,22.Меньшее число равно .Большее число равно...

Популярные вопросы