Исследовать сходимость ряда
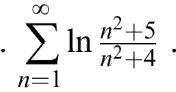
Другие вопросы по теме Математика
Популярные вопросы
- Дискуссия глаза - зеркало души или зеркало души - губы...
2 - Вкругу с центром в точке о проведено хорду ав и диаметр вс. найдите углы...
2 - :1)вычислите массу 10%-ного раствора серной кислоты,который потребуется...
3 - Морфологический разбор слова плёлся ....
2 - При взаимодействии раствора карбоната натрия массой 250 г (массовая доля...
2 - Решить : 4 cos 20 gr + 12 cos 520 gr числитель знаменатель -2cos (340 gr...
3 - А)31,8дм-902,3мм+0,5м; б)(8га 3а-841а 50м(2): 4,5): 1,54+26000000...
2 - 2)6,72 литра н.у углекислого газа пропустили через раствор гидроксида натрия....
2 - X+2y=-2; 3x-y=8 решить подстановки...
1 - Где закончилась отечественная война...
2
Сходится
Пошаговое объяснение:
Пусть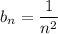 . При этом
. При этом 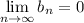 .
.
Тогда, так как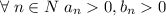 и ряд
и ряд 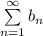 сходится, то, по предельному признаку сравнения, ряд
сходится, то, по предельному признаку сравнения, ряд 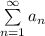 также сходится.
также сходится.