Исследовать ряды на сходимость
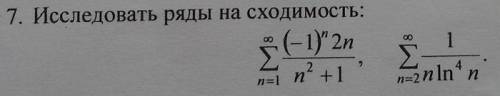
Другие вопросы по теме Математика
Популярные вопросы
- Здравствуйте. Нужна . Я изучаю параметры, но у меня это очень плохо получается....
3 - 10 римеров Золотого правила морали...
2 - ответьте на вопросы 1. Чем объясняется необходимость решения глобальных проблем...
2 - Решите методом подстановки систему управления x+2y=4...
1 - 15y+8=17−120y.подскажите ...
2 - Чи може паралельною проекцією двох мимобіжних прямих бути пара паралельних прямих?...
1 - В саду растут 13 роз и 14 гвоздики.Девочка сорвала 13 цветков ответь на вопросы...
3 - Ad перпендикуляр к плоскости a Ab и Ac наклонные AB =15 BD =9 DC =5 найдите длину...
2 - С какими государствами взаимодействовали западные сарматыи восточные сармаьы...
3 - У МЕНЯ СОЧ 2 тапс билим ленд СОЧ қазақ тілі 5 сынып >...
3
Это числовой знакочередующийся ряд, исследуем его по признаку Лейбница.По первому признаку Лейбница каждый последующий член ряда по абсолютной величине должен быть меньше предыдущего, т.е. для нашего ряда это условие выполняется
По второму признаку Лейбница предел ряда должен стремится к 0.
Таким образом, рассматриваемый ряд сходится. Теперь нужно исследовать на абсолютной и условной сходимости ряда. Возьмём данный ряд по модулю
По интегральному признаку:
Несобственный интеграл сходится, а значит сходится и рассматриваемый ряд