Исследовать ряд на сходимость с объяснением
(2n+1) tg П/3^n
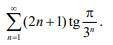
Другие вопросы по теме Математика
Популярные вопросы
- Л.андреев петька на даче .(составить 5 вопросов к тексту)...
2 - Найди объем прямоугольного параллелепипеда если его длинна равна...
3 - Разгадайте шарады. три буквы-термин при игре. другие три-победный...
3 - Вставьте артикли, где это необходимо. 1. i didn’t understand last...
2 - Для того, чтобы связать свитер, хозяйке нужно 600 граммов шерстяной...
3 - Составьте небольшое сочинение о зиме, используя наречия: холодно,...
2 - Вычислите сколько соли и воды необходимо взять для приготовления...
1 - !составьте план ответа по теме “общяя характиристика червей”...
1 - Много-один ряды-ряд народы-народ выдели общую(одинаковую) часть...
1 - Вкаком веке был открыт университет ломоносова?...
3
Признак сравнения в предельной форме говорит, что для положительных рядов мы можем заменить члены ряда на эквивалентные выражения (это когда предел отношения равен 1), не меняя факта сходимости или расходимости. В данном случае это означает переход к ряду с членами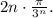 Чтобы стало еще комфортнее, можно отбросить постоянный множитель
Чтобы стало еще комфортнее, можно отбросить постоянный множитель 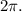
Итак, имеем ряд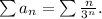 Для его исследования применим признак Даламбера.
Для его исследования применим признак Даламбера.