1. Математика
  2. исследовать несобственные

исследовать несобственные интегралы на сходимость, пример: 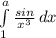\int\limits^a_1 {\frac{sin}{x^3} } \, dx . Вместо а - ∞. ответ: сходится

revon revon    1   03.07.2021 13:08    2

Ответы
никита3473 никита3473  02.08.2021 13:49

Сходится

Пошаговое объяснение:

$\int\limits_1^\infty \dfrac{sinx}{x^3}dx

Особая точка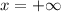 x=+\infty.

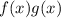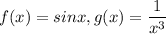Подынтегральная функция представима в виде f(x)g(x), где f(x)=sinx,g(x)=\dfrac{1}{x^3}.

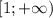1) f(x) непрерывна на [1;+\infty).

2) $\left|\int\limits_1^A sinxdx\right|=\left|-cosx\right|\limits_1^A=\left|cos1-cosA\right|\leq |cos1|+|cosA|< 2 \;\;\forall A\geq 1

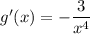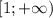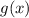3) g'(x)=-\dfrac{3}{x^4} непрерывна на [1;+\infty). При этом g'(x), а значит g(x) монотонно убывает.

4) \lim\limits_{x\to\infty}g(x)=0

Значит, интеграл сходится по признаку Дирихле.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
аня535767 аня535767  28.11.2021 15:58
6 целых 9/16 + 2 целых 3/11...
MainkraeTV MainkraeTV  28.11.2021 15:58
78–3(5+4(x–3))+10 = 6+5(3x–1)...
круасана круасана  28.11.2021 15:59
с заданиями(на фотографии)...
dygbejs dygbejs  28.11.2021 15:59
Реши задачу. В классе 27 учащихся. Одна третья часть девочек . Сколько девочек в классе?...
nikitalandsberg nikitalandsberg  28.11.2021 16:00
Задача. На полицях у бібліотеці стоять словники число яких менше ніж 130 .Скільки стоїть словників ,якщо відомо,що їх можна розставляти по 15,по 6,по 8 шт...
ivan200302 ivan200302  28.11.2021 16:01
решить (к Роботу Роботовичу, у меня это в электронном дневнике как домашнее задание,)...
eminka1 eminka1  28.11.2021 16:01
Напишите вместо x такое натуральное число, чтобы получилось . верное неравенство...
alesia4 alesia4  28.11.2021 16:01
Всего 27 детей,из них 12 ходят на вокал,19 на танцы,5 в обоих кружках,сколько из них не ходят в кружки...
dashikryb dashikryb  28.11.2021 16:02
6/11(15/20-11/36)×21/29+ 6 6/7÷16/21...
варя388 варя388  28.11.2021 16:02
1. Запишите натуральные числа: 1) 3; 2) 5; 3) 8; 4) 9 в виде суммы двух смешанных чисел, знаменатели которых равим 7 и 7....

Популярные вопросы