Исследовать на сходимость ряд
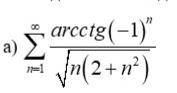
Другие вопросы по теме Математика
Популярные вопросы
- 23*3+14*2=?43*2-13*3=?200-44*2+126=? надо столбиком...
3 - Упование выдвинули персы через своих послов до начала греко-персидских...
3 - А3 Треугольники ABO и DCO подобны и 20CD . - 20AD. Определите, какая...
2 - Разбейте текст на смысловые части и озаглавьте каждую часть ключевым...
3 - Увеличите 38 в 10 раз и прибавьте к ближайшему круглому числу...
1 - Спартитату нельзя было заниматься никаким физическим или умственным...
3 - Где находится Пеиро орхидея На какой части карты где гео статуя архонта?...
3 - 1. Дана целочисленная матрица А(MxN), заполненная случайными числами....
1 - Перевод текста ! Немецкий язык 5 класс ! Страница 115 и 116...
3 - АИ 1-тапсырма. Сұрақтарға жауап бер.САРАҢ БАЙ НЕ ДЕДІ?АЛДАРКӨСЕ НЕ...
2
Абсолютно сходится
Пошаговое объяснение:
Исследуем на сходимость ряд, состоящий из модулей слагаемых исходного ряда: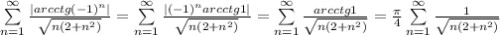
Будем использовать признак сравнения, а именно будем сравнивать этот ряд (с точностью до множителя перед знаком суммы) с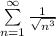
Посчитаем предел отношения членов этих рядов:
Этот предел конечный и не равен 0, значит, ряды сходятся или расходятся одновременно. Так как второй ряд имеет вид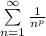 , где p>1, то он сходится, а значит сходится и исходный ряд, причем абсолютно.
, где p>1, то он сходится, а значит сходится и исходный ряд, причем абсолютно.