Исследовать функцию Z= x^2 + 2y^2 + 2xy + 4y-2 на экстремум
Другие вопросы по теме Математика
Популярные вопросы
- Сравните дроби: а) 1/2 и 1/3б)5/11 и 7/11в)1/2 и 2/3 г) 2/5 и...
3 - Дотронувшись рукой до поверхности двух тел,вам показалось,что...
3 - Кто считался героем в древнегреческой мифологии?...
2 - Решить уравнение 6(2х+0,5)=8х-(3х+4)...
3 - Построй и запиши обращение к незнакомому человеку чтобы узнать:...
1 - Названия народов, представители которых населяют твой край...
3 - Как проверит приставку в слове побольше...
2 - Что принимают за тело отсчета, когда говорят земля движется по...
1 - Дано: абсд-паралеллограм,угол 1=углу 2=1: 4 найти: углы паролелограмма...
2 - Используя план местности (рис.2), определите расстояние от а...
3
Проверка:
Проверка:
В точке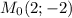 функция имеет экстремум – минимум
функция имеет экстремум – минимум