Исследовать функцию y=(x-1)^2/x^2, (попытался показать как она выглядит через местную вставку уравнений, без понятия если будет работать как надо)

нужны:

1.Область определения D(y) и область допустимых значений E(y) функции.

2.Четность, нечетность функции.

3.Точки пересечения с осями.

4.Асимптоты функции.

5.Экстремумы и интервалы монотонности.

6.Точки перегиба и промежутки выпуклости, вогнутости.

(ссылка на пример исследований)
https://www.webmath.ru/poleznoe/formules_8_26.php

Пошаговое объяснение:

для исследования функции понадобятся первая и вторая производные. я их сразу найду, чтобы потом не повторяться

теперь поехали

1. Область определения D(y) и область допустимых значений E(y) функции.

D(y)= (x∈ R ; x≠ 0)

 E(y) = ( y∈ R ; y ≥0)

2 Четность, нечетность функции.

эта функция не является четной и не является нечетной

четность  y(-x) = y(x) смотрим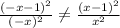  

нечетность y(-x) = -y(x)  смотрим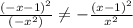  

3.Точки пересечения с осями. или так называемые нули функции

y' = 0;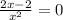     ⇒  x₀ = 1  y(1)=0;  точка пересечения с осью ОХ   К(1;0)

4.Асимптоты функции

ищем в виде y = ax +b

из определения асимптоты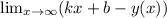  

найдем  к и b

мы получили горизонтальную асимптоту у = 1

теперь вртикальная асимптота

точка разрыва у нас х₀ = 0

посмотрим, какого она рода и является ли х = 0  асимптотой

x= 0  есть вертикальная асимптота

5.Экстремумы и интервалы монотонности.

критические точки, (они же точки экстремума, они же потенциальные точки смены знака)  ищутся y' = 0

  ⇒  x₁ = 1 - точка экстремума.

используем вторую производную, чтобы определить точка минимума или точка максимума  

 y''(1)=2 > 0  значит точка x₁ = 1 точка минимума функции.

к этой точке добавим точку разрыва х₀ = 0

и вот мы получили интервалы возрастания и убывания функции

смотрим знак производной на интервале. берем любую точку ∈ интервалу и вычисляем значение производной

(-∞; 0) y'(-1) = 4 > 0 - функция возрастает

(0; 1)  y'(0,5) = -8 < 0 - функция убывает

(1; +∞) y'(2) = 0.25 > 0 - функция возрастает

6.Точки перегиба и промежутки выпуклости, вогнутости.

 ⇒  x₁ = 1.5 точка перегиба

к этой точке добавим точку разрыва  x₀ = 0 - потенциальную точку перегиба

и вот мы получили интервалы перегибов функции

(-∞; 0) y''(-1) = 10 > 0 - функция вогнута

(0; 1,5)  y''(1) = 2  > 0 - функция вогнута

(1.5; +∞) y''(2) = -0.25 < 0 - функция выпукла

 x₁ = 1.5 -да, а вот   x₁ = 1.5 нет тогда у(1,5) = 1/9

т.о точка прегиба M(3/2; 1/9)