Исследовать функцию на экстремум и построить схематич график: y=x^3-3x^2+5

Находим производную.

y' = (x^3-3x^2+5)' = 3x^2 - 6x 

Приравниваем к нулю

3x^2 - 6x = 0 

Находим дискриминат

D = b^2 - 4ac = (-6)^2 - 4 * 3 * 0 = 36

x1 =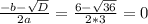 

x2 =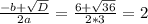  - критические точки

f(max) = f(0) = 0^3 - 3* 0^2 + 5 = 5

f(min) = f(2) = 2^3 - 3 * 2^2 + 5 = 1

График можно построить тут

http://graph.reshish.ru/