Исследовать функцию (3*(x^2-x+1))/(x^2+x+1)

ИССЛЕДОВАНИЕ

1.Область определения D(x) - деления на 0 нет- непрерывная.

Х∈(-∞;+∞) - вертикальных асимптот - нет.

2. Пересечение с осью Х. Y=0 - нет. 

Пересечение с осью У.  У(0) = 3. 

4. Поведение на бесконечности - горизонтальная асимптота.

. 

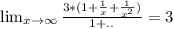
5. Исследование на чётность.Y(-x)  ≠ Y(x).

Функция ни чётная ни нечётная. 

6. Производная функции - Y'(x).

(тихий ужас)

Корни при Х= +/-1. (без комментариев)

7. Локальные экстремумы. Максимум Ymax(-1)= 9, минимум – Ymin(1)=.1 

8. Интервалы возрастания и убывания. 

Возрастает - Х∈(-∞;-1)∪(1;+∞) , убывает = Х∈(-1;1). 

8. Вторая производная - Y"(x) = -6*(x-3)/x⁴

Корень производной - точка перегиба Y"(x)= 0. при х =0.

9. Выпуклая “горка» Х∈(-∞;0), Вогнутая – «ложка» Х∈(0;+∞). 

10. График в приложении.