Используя теорему Безу, найдите остаток от деления многочлена: Количество связей: 3
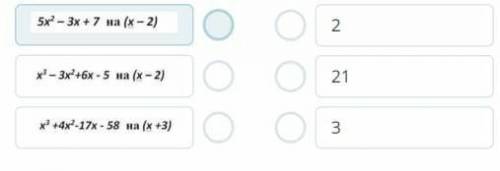
5x^2 - 3x +7 на (х-2)
x^3- 3x^2+6x -5 на (x- 2)
x^3 +4x^2-17х-58 на (х +3)
2
3
21
Другие вопросы по теме Математика
Популярные вопросы
- Второстепенные чл предложения которые произносятся с интонацией перечисления...
3 - Что, по вашему мнению, определяет самобытность русской литературной...
1 - Составить сообщение из данных тем по геометрии! 1. «Арифметика фигур»...
1 - Вычисли y(2), если y(j)= −j−7,2. ...
3 - Произведение Маленький принц 2.Задание основано на знании текста...
1 - Рассчитать жесткость воды в 1л, 20 ммоль СаCl2, 0,01 моль Са(НСО3)2....
2 - сделать 12 номер сделать 12 номер >...
3 - Прочитать параграф Московское государство и его соседи во второй...
1 - 1.Определить скорость химической реакции 2NO+O2=2NO2, если к=1,4...
2 - Мне нужно написать Твір « один рік після вірусу...
1
Пошаговое объяснение:
* * * * * * * * * * * * * * * * * * * * * * *
Используя теорему Безу, найдите остаток от деления многочлена x³+2x² -13x+10 на x - 2.
ответ: 0.
Объяснение: P(x) =(x - a)*Q(x) +R ⇒ R = P(a)
x³+2x² - 13x+10 = (x - 2) * (Ax²+Bx +C) + R ; R_остаток
x =2. 2³ +2*2² -13*2 +10 = (2-2) * (Ax²+Bx +C) + R ⇒ R =0
* * * * * * * * * * * * * * * * * * * * * * * *
x=2 является корнем многочлена P(x) = x³+2x² -13x+10
т.к. 2³ +2*2² -13*2 +10 =8+ 8 - 26 +10 = 0
* * * ! 2 является делителем свободного члена_10 * * *
следовательно x³+2x² -13x+10 делится на (x-2) ,без остатка
* * * остаток равен нулю * * *
x³+2x²-13x+10 = (x -2) (x² +4x - 5)
* * * x³+2x²-13x+10 =x³ - 2x²+4x² -8x -5x +10 =
x²(x-2) +4x(x -2) -5(x-2) = (x-2) (x²+4x -5) = (x-2)(x-1)(x+5)
* * * Делить можно а также столбиком или по схеме Горнера * * *
корни { -5 ; 1 ; 2} являются делителями свободного члена