Используя свойства числа сочетаний, найти 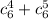
Другие вопросы по теме Математика
Популярные вопросы
- Клиент получает в банке кредитную карту.четыре последние цифры номера карты...
2 - Оля 7 лет старше кати сколько лет каждой девочки если вместе им 23 года...
1 - Найди корень уравнения: −14-0,2b=-18 . b= ....
1 - Установите соответствие между событиями и датами. события а) учреждение...
3 - даны персидские слова в записи латинскими буквами и их переводы на язык...
2 - Снайти такой х , при котором оба выражения х²-10х+13 и х²+2х-4 отрицательные...
1 - Морфологический разбор слова умнейшим....
1 - Решить тест, 25 . 1. выберите правильную форму глаго-ла “to be”: there...
2 - 1.определи величины углов треугольника dec, если ∡ d : ∡ e : ∡ c = 3 :...
1 - Германия на пути к европейскому лидерству краткий конспект...
1
Одно из свойств гласит:
Согласно данному свойству,
Подставим значения в формулу сочетаний:
Раскроем факториалы:
Упростим выражение
Произведем вычисления:
Сложим полученные значения:
Таким образом,