Используя решение примера (на фото рисунок 1) решите уравнение(рисунок 2):

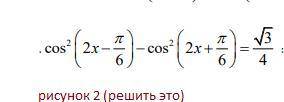
Другие вопросы по теме Математика
Популярные вопросы
- Какие качества необходимы талантливому собеседнику?...
3 - Весы кулона-кавендиша, что это и как работает?...
1 - Напишите эссе на тему дорога к родине не менее 50 слов...
1 - Сочинить небольшую сценку по теме зимние забавы обж....
3 - Иван иванович отправился из дому на рыбную ловлю.три часа он ехал поездом со...
2 - Экологические проблемы и их решение? заранее ))...
1 - Нужно решать с дано и с решением 1) как будет двигаться тело массой 8кг под действием...
2 - Напишите эссе на тему богатство мира неменее 50 слов...
3 - Впервом ящике 30 кг картошки. во втором-на 6 кг больше, чем первом, ф в третьем...
1 - Какой опыт из политической жизни(россии,планеты) xx-xxl вв. могут извлечь будущие...
3
x = (-π)/24 - πk/2
Пошаговое объяснение:
cos^2(2x - π/6) - cos^2(2x + π/6) = sqrt(3)/4;
(cos 2x * cos π/6 + sin 2x * sin π/6)^2 - (cos 2x * cos π/6 - sin 2x * sin π/6)^2 = sqrt(3)/4;
cos π/6 = sqrt(3)/2; sin π/6 = 1/2;
Умножаем сразу обе части сразу на 4
(cos 2x * sqrt(3) + sin 2x)^2 - (cos 2x * sqrt(3) - sin 2x)^2 = sqrt(3);
Используя разность квадратов, получаем:
2sqrt(3) * cos 2x * (-2) * sin 2x = sqrt(3);
2sin 2x * cos 2x = (-1/2);
sin 4x = (-1/2);
Вносим знак, получаем
sin (-4x) = sin (π/6 + 2πk);
-4x = π/6 + 2πk;
x = (-π)/24 - πk/2