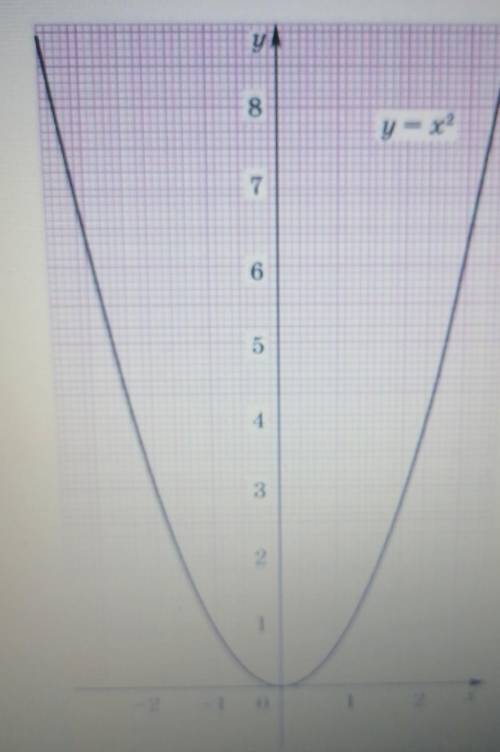
Используя график функции y = ? (см. рис. 9), найди с точностью до 0, 1 корни уравнения: а) t2 = 2, 5,
б) х2 = 3, 5.

Добрый день! Я рад представиться вам в роли школьного учителя и помочь вам разобраться с задачей.

Для решения этой задачи, мы должны использовать график функции, заданной уравнением y = ?. Однако, на приведенном рисунке график не указан, поэтому мы не можем определить функциональную зависимость.

Чтобы решить уравнение t^2 = 2.5, нам необходимо найти значение t, при котором квадрат этого значения равен 2.5. В данном случае, у нас нет возможности использовать график функции, поэтому придется прибегнуть к использованию математических методов.

Для начала, можно попробовать численные методы, такие как подстановка различных значений t и проверка условия t^2 = 2.5. Когда мы подставим различные значения t, мы найдем несколько точных решений. Однако, мы ищем ответ с точностью до 0.1. Поэтому, нам потребуется использовать другой метод.

Еще один метод, который мы можем использовать, это метод бисекции. Он основан на теореме о промежуточных значениях и позволяет нам найти решение уравнения с заданной точностью.

Для того, чтобы использовать метод бисекции, нам необходимо выделить интервалы, где функция меняет знак. На графике, это означает нахождение точек пересечения с осью x. Затем мы делим интервал пополам и выбираем половину интервала, где функция меняет знак. Повторяем этот процесс до тех пор, пока не достигнем нужной точности.

Для уравнения t^2 = 2.5, мы можем разделить интервал от -3 до 3 пополам и получить интервалы [-3,0] и [0,3], где функция меняет знак. Затем мы можем продолжать делить выбранные интервалы пополам, чтобы найти значения t с заданной точностью.

Аналогичным образом, мы можем решить уравнение х^2 = 3.5, используя метод бисекции. На этом этапе, для определения интервалов, где функция меняет знак, мы должны знать график функции y = ?. Однако, на приведенном рисунке график не указан, поэтому мы не можем продолжить решение.

В целом, для решения уравнений с заданной точностью, мы можем использовать численные или графические методы. При отсутствии графика функции, мы можем попробовать использовать численные методы, такие как подстановка значений и метод бисекции.