Используя графический метод , решить задачу линейного програмирувания
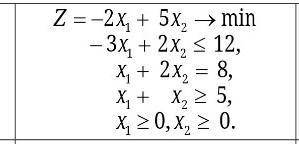
Другие вопросы по теме Математика
Популярные вопросы
- Найти координаты звёзд: 1) альфа малой медведицы; 2) бета кассиопеи; 3)альфа...
3 - Задание №2. Найдите в тексте сказуемые, выраженные глаголом, определите...
1 - с алгеброй При каких значениях х имеет смысл выражение (к этому выражению...
3 - Английский язык RAINBOW ENGLISH 7 класс диагностические работы О. В. Афанасьева...
1 - Школярі побували на екскурсії у київському природознавчому музеї. Повертаючись...
2 - с исскуством, 8класс. Поставлю максимум ....
1 - найти всё, что требуется. Дано: U=100B, R1=R2=10 Ом, X(C3) =4 Ом, X(LI)...
1 - Назовите 4х пророков учения Ииеуса Христа?...
2 - 2. Дополните схему В начале XVII в. на территорию Казахского ханства периодически...
1 - I didn t Spanish and Kate for me. 2 My teacher thinks that grammar are...
2
Пошаговое объяснение:
1) строим область допустимых решений. , т.е. решаем графически систему неравенств.
строим каждую прямую и определим полуплоскости, заданные неравенствами
2) где все полуплоскости пересекаются, там и есть наша область допустимых решений
на графике я ее заштриховала, и отметила точки, определяющие "углы" области
3) теперь целевая функция задачи Z = -2x1+5x2 → min.
нарисуем график Z= -2x1+5x2 (зеленая линия через начало координат) его и будем двигать для поиска решений
вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации F(X). начало вектора – точка (0; 0), конец – точка (-2;5), но нам надо минимизация, поэтому прямую
Z = -2x1+5x2 будем двигать по вектору, но в противоположном направлении. (т.е. будем ее параллельным образом двигать вниз) до первого касания обозначенной области
в конце концов, эта прямая дойдет до нижней точки (8;0)
сюда и найдем минимальное значение целевой функции:
Z(x) = -2*8 + 5*0 = -16