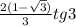используя формулы синуса, косинуса, тангенса, котангенса суммы и разности двух углов, а также формулы двойных углов упростить выражение. буду очень признательна за подробное решение
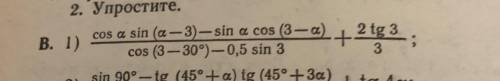
Популярные вопросы
- По каким признакам различают ткани у организмов?...
2 - Решить катер шёл 2часа по течению и 3 часа против течения. какой путь...
1 - Переделайте личные предложения в безличные 1ночью в саду ветер посбивал...
3 - Какая местность находится по координатам 50 градусов северной широты...
2 - Бабушка своим внукам послала 4 ящика яблок, а племянникам -3 таких же...
1 - Найдите значение функции y=3x-11÷2+x при значении аргумента x=4...
2 - Чему равна масса 2 млль углекислого газа co 2...
3 - Предложение с тире между подлежащим и сказуемым ....
2 - Краткое сообщение на темы 1.одноклеочные организмы 2.мышечная и нервная...
3 - Рассчитать какой объём газа и какое число молекул в 28 граммах nh3,n2....
1
1) Числитель первой дроби (синус разности):
2) Знаменатель первой дроби (косинус разности):
3) Первая дробь (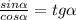 ):
):
4)
ответ: