иследование функции на непрерывность
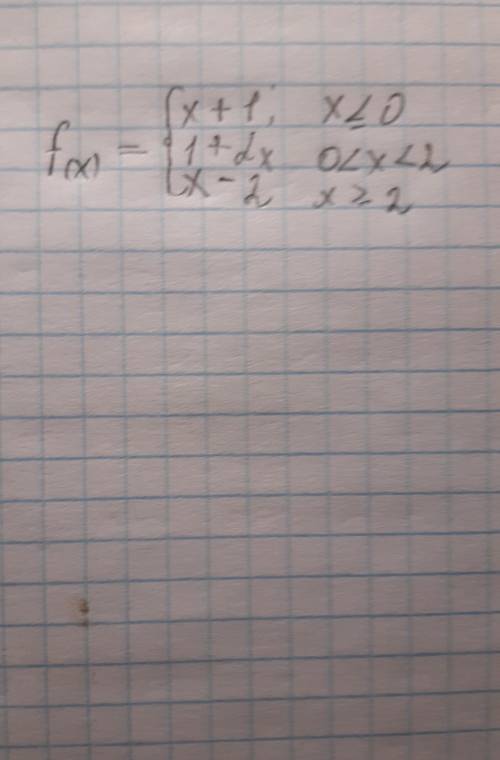
Другие вопросы по теме Математика
Популярные вопросы
- Обчисліть об єм водню (н.у.), що виділиться під час взаємодії калію з етиленгліколем...
2 - 6. Розв яжи задачу. ( ) Пароплав пройшов відстань 16 км за течією ріки та...
2 - В первом примере нужно исследовать функцию на чётность...
3 - В какой сказке используется хкдожественный приём сновидение?...
3 - Назвіть основні ремесла в середньовіччі яка їх роль в розвитку міста...
2 - Спиши, вставив окончания, укажи спряжения. Зимой солнце свет...т, но не...
3 - разобрать по составу: Крутой подъем, звонкие ручьи, интересное объявление,...
3 - Написать отличие и сходства воссалов от Сеньёров? МИНИМУМ 5 СХОДСТВ И 5...
2 - Появился бесплатный б0т, который не требует подписку для просмотра ответов...
2 - Як зростання цін вироблених товарів впливає на заробітну плату?...
2
это точки - края определения кусочно-заданой функции
точки: х = 0 и х = 2
1. Точка х = 01. В данной точке существует значение функции?
Да,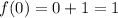
2. Выполняется равенство односторонних пределов?
Да,
3. Существует ли предел в этой точке и конечен ли он?
Да,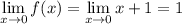
Вывод: в точке 0 функция непрерывна2. Точка х = 21. В данной точке существует значение функции?
Да,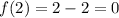
2. Выполняется равенство односторонних пределов?
Нет,
В этой точке функция терпит разрыв первого рода, а значит не является непрерывной