Интеграл. Продолжаем пировать
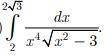
Другие вопросы по теме Математика
Популярные вопросы
- Дайте определение следуйщих понятий : колония , эллада, эллины. 19 ....
1 - Конкурс волшебный сундучок учатся 23 январь в школу они набрали вместе 7510...
1 - Дополнительные занятия древних славян...
2 - Разберите предложения по члена предложения вчера к работе приступил новый менеджер...
1 - Для ремонта школы 900 шт. белых и красных кирпичей, одинаковых по массе.масса...
2 - 2.укажите все пары противоположных чисел: 1) – ( – 6) и 6; 2) – ( – ) и ; 3)...
1 - Придумать предлож с любым словом в котором есть разделит мягкий знак. ручей,...
3 - Такая греза не дай господи объясни значение...
3 - Из 128 изделий прикладного исскуства , показанных на выставке , 3 \ 4 составляют...
2 - Если делимое разделить на значение часного ,то палучится...
2
Пошаговое объяснение:
не судите строго
III. ИНТЕГРАЛЫ ОТ БИНОМИАЛЬНЫХ ДИФФЕРЕНЦИАЛОВ
Так называются интегралы вида
∫x^m(a+bx^n)^p, (9,8)
где m, n, p —
любые рациональные числа;
а и Ь —
какие угодно постоянные, не равные нулю
Подынтегральное выражение называется биномиальным дифференциалом.
1
Кoнечно, предполагается, что числа m, n, p не все целые. Если бы все
они были целыми, то вопрос свелся бы к интегрированию суммы степенных
функций.
П. Л. Чебышев доказал, что только в трех случаях этот
интеграл может быть выражен в конечном виде через
алгебраические, логарифмические и обратные круговые функции:
1) р —
целое число, которое может быть положительным, отри-
отрицательным или равным нулю. В этом случае применяется под-
cтановка
х =y^s
где s —
общее наименьшее кратное знаменателей дробей m и n.
Это простейший случай: дело сводится к интегрированию суммы
степенных функций.
2) - целое число. Здесь следует применить подстановку
а + bx^n = y^s
где s — знаменатель дроби р.
3) (m+1)/n +р —целое число. В этом случае применяют подстановку
ах^(-n)+b=y^s
где s — знаменатель дроби р.
Других случаев интегрируемости биномиальных дифференциалов, кроме перечисленных, нет. Интересно отметить, что они были
известны еще Ньютону, а Эйлер указал приведенные выше под-
подстановки. Однако только П. Л. Чебышев доказал, что эти случаи
интегрируемости являются единственными и что в других случаях
интеграл (9,8) не может быть выражен при элементарных
функций.
у нас m=-4, n=2, p=-1/2
(-4+1)/2-1/2=-3/2-1/2=-2 - cлучай 3