Имеются два сосуда, содержащие 30 кг и 42 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 40 % кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 37 % кислоты. Сколько процентов кислоты содержится во втором растворе?
Другие вопросы по теме Математика
Популярные вопросы
- Сторона основи правильної трикутної піраміди дорівнює 3 см, а апофема...
3 - На сколько градусов изменится часовая стрелка если секундная на 216...
3 - Назови государственные праздники России. 1)День России 2)День...
2 - 2. Подберите к каждому эпизоду подходящую цитату изтекста...
2 - Вкажіть, що з перерахованого нижче належить до екранних мистецтв (ДЕКІЛЬКА...
1 - Комментарии к решению: Из треугольника AKD найдите KD Из треугольника...
1 - 1.Н.В. Гоголь « Тарас Бульба» Почему Тарас казнит Андрия? 2. М. Горький...
3 - Чень Упражнение 1. Поставьте глаголы в скобках в Present Perfect. 1....
3 - На полке 11 книг, из них 7 детективов. Выбрали 5 книг. Найти вероятность...
1 - Определи координаты точек пересечения графиков функций y=x2+1,4x и...
2
Пусть кг - кислоты в первом растворе в первом сосуде;
кг - кислоты в первом растворе в первом сосуде;
тогда
1)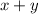 кг - кислоты в растворе, полученном путем слияния первых двух растворов из обоих сосудов:
кг - кислоты в растворе, полученном путем слияния первых двух растворов из обоих сосудов:
Получаем первое уравнение:
2) 37% = 0,37
Получаем второе уравнение:
3) Решаем систему:
Из первого уравнения выразим
и подставим во второе уравнение:
Во втором растворе 21 кг кислоты
Выразим это в процентном отношении:
ответ: 50%