Имеется машина Тьюринга с внешним алфавитом А = {a0, 1}, алфавитом внутренних состояний Q = {q0, q1} и программой (таблица)
Определить, в какое слово перерабатывает машина каждое из следующих слов, если она находится в начальном состоянии q и обозревает указанную ячейку, считая слева:
11а0111а01
Изобразите схематически последовательность конфигураций, возникающих на ленте на каждом такте работы машины.
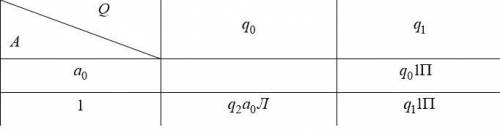
Другие вопросы по теме Математика
Популярные вопросы
- Найти корни квадрата 3-х члена б) x3-16x...
3 - Цепочка превращений веществ mgo— mg(oh)2– mg(no3)— mgco3...
2 - Видимая звездная величина кастора 2m. вычислите расстояние до звезды в световых...
2 - Это все одни предрассудки грамматическая основа...
2 - Пьер де кубертен в журнале опубликовал статью возрождение олимпийских игр...
3 - Які процеси відбувалися в економіці україни першої половини 19ст...
1 - Может ли равнобедренная трапеция быть гранью многогранника ...
3 - Назовите причины войны между испанией и кратко...
1 - Найдите значение выражения 2,3*(b-3)-4*(6,2-b) при b=2...
3 - Максимальное кол-во . надо, до урока 2 часа. (...
1
Данная машина Тьюринга имеет два внутренних состояния: q0 и q1, и два символа во внешнем алфавите: a0 и 1. Также, дана программа (таблица), которая показывает, какой символ написать на ленте и какое внутреннее состояние установить в зависимости от текущего внешнего символа и текущего внутреннего состояния.
Давайте проследим последовательность конфигураций машины для данного слова 11а0111а01 при начальном состоянии q и обозревании указанной ячейки, считая слева. Для удобства, обозначим пустые ячейки символом "_".
1.
Начальная конфигурация: q 1 1 a0 0 1 1 a0 1 _
2.
По программе, при такой конфигурации, машина должна написать a0 на ячейку перед текущей и переместиться вправо.
Конфигурация после 1 такта: q0 a0 1 1 a0 1 _
3.
По программе, при такой конфигурации, машина должна перейти в состояние q1 и переместиться вправо.
Конфигурация после 2 такта: q1 a0 a0 1 1 a0 1 _
4.
По программе, при такой конфигурации, машина должна оставить a0 на месте и переместиться вправо.
Конфигурация после 3 такта: q1 a0 a0 a0 1 1 a0 1 _
5.
По программе, при такой конфигурации, машина должна перейти в состояние q0 и переместиться вправо.
Конфигурация после 4 такта: q0 a0 a0 a0 a0 1 1 a0 1 _
6.
По программе, при такой конфигурации, машина должна записать a0 на ячейку перед текущей и переместиться вправо.
Конфигурация после 5 такта: q0 a0 a0 a0 a0 a0 1 1 a0 1 _
7.
По программе, при такой конфигурации, машина должна перейти в состояние q0 и переместиться вправо.
Конфигурация после 6 такта: q0 a0 a0 a0 a0 a0 a0 1 1 a0 1 _
8.
По программе, при такой конфигурации, машина должна записать 1 на текущую ячейку и переместиться вправо.
Конфигурация после 7 такта: q0 a0 a0 a0 a0 a0 a0 1 1 1 a0 1 _
9.
По программе, при такой конфигурации, машина должна перейти в состояние q1 и переместиться вправо.
Конфигурация после 8 такта: q1 a0 a0 a0 a0 a0 a0 1 1 1 a0 1 _
10.
По программе, при такой конфигурации, машина должна записать 1 на текущую ячейку и переместиться вправо.
Конфигурация после 9 такта: q1 a0 a0 a0 a0 a0 a0 1 1 1 1 a0 1 _
11.
По программе, при такой конфигурации, машина должна перейти в состояние q1 и переместиться вправо.
Конфигурация после 10 такта: q1 a0 a0 a0 a0 a0 a0 1 1 1 1 1 a0 1 _
12.
По программе, при такой конфигурации, машина должна записать 1 на текущую ячейку и оставить состояние без изменений.
Конфигурация после 11 такта: q1 a0 a0 a0 a0 a0 a0 1 1 1 1 1 1 a0 1 _
13.
По программе, при такой конфигурации, машина должна остановиться, так как нет инструкций для данного состояния и символа.
Конечная конфигурация: q1 a0 a0 a0 a0 a0 a0 1 1 1 1 1 1 a0 1 _
Таким образом, машина Тьюринга перерабатывает слово 11а0111а01 в последовательность символов a0 a0 a0 a0 a0 a0 1 1 1 1 1 1 a0 1 _, при нахождении в начальном состоянии q и обозревании указанной ячейки, считая слева.
Чтобы изобразить схематически последовательность конфигураций, возникающих на ленте на каждом такте работы машины, можно использовать специальные символы для обозначения состояний и символов на ленте. Например, q0 и q1 можно обозначить как q0 и q1, а символы a0 и 1 можно обозначить как a0 и 1. Также, можно использовать стрелки или указатели для обозначения перемещения на ленте. В данном случае, начальная конфигурация будет выглядеть следующим образом:
q 1 1 a0 0 1 1 a0 1 _
А каждая следующая конфигурация будет получаться путем изменения соответствующих символов и перемещения указателя на ленте.
Надеюсь, что данное пошаговое решение и схематическое представление помогут вам понять, как работает данная машина Тьюринга и как она перерабатывает данное слово.