И еще второй вопрос в профиле
Другие вопросы по теме Математика
Популярные вопросы
- Твір клим джура захисник світу...
3 - На двери одного из подъездов многоквартирного дома висит табличка...
1 - Контрольная работа по теме обособленные члены предложения 2 вариант...
3 - Почему вставили подчеркнутые слова, и какого времени каждое предложение....
3 - Яка з наведених точок належить осі оху м(-1; 6; 2) к(0; 3; -9)...
1 - Твір мініатюра прийшла весна із ставними словами 5-6 речень...
2 - Много напишите вопросы и отрицания к этим предложениям! . заранее...
3 - Как вы считаете, какой прихода к власти монарха был более благоприятным...
3 - Очём плачут лошоди монолог воспоминания рассказчика...
2 - Мне нужно знать что такое гл (сакращённое)...
2
Объединяем оба ответа в один , получаем :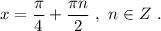
Объединяем оба ответа в один, получаем :