И что!??? как они это вообще решили? нигде нет пояснения! даже видео не нашла

Другие вопросы по теме Математика
Популярные вопросы
- Укажіть точку, що належить графіку рівнянння х + у = 6а(2:3)б(2:4)в(-2:-4)г(3:4)...
2 - Сделайте,что сможете,желательно задачи 7 и 2❤️...
1 - Ребят с домашкой по химии, хотя бы одно задание...
2 - Как гуси Рим нужен конспект на презинтацию...
3 - Как вы понимаете эти строки?(5-10 предложений)...
2 - На чиєму боці письменник? - Яке ваше перше враження від Маленького...
1 - ЗАРАНЕЕ Сторона квадрата равна 1. На рисунках проведены окруж-ности,...
3 - Вычислите энергию связи кислорода 8 18 О. Масса атома кислорода...
3 - Написати невеличкий роздум на тему причини ,що призвели людство...
3 - Реши уравнение: −35:|x|=0,03−7,03 ответ: x1= x2=...
2
А) Рассмотрим число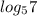 . Попробуем подобрать такие числа, записанные в виде логарифмов, значения которых мы точно знаем, и между которыми располагается заданное число.
. Попробуем подобрать такие числа, записанные в виде логарифмов, значения которых мы точно знаем, и между которыми располагается заданное число.
Так как известно, что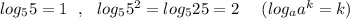 , и
, и
выполняется неравенство 5<7<25 , причём логарифмическая функция по основанию 5 возрастающая ( то есть чем больше значение аргумента, тем больше значение функции), то получаем неравенство:
Б) Выделим целую часть у неправильной дроби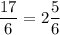 . Это число немногим больше 2, но меньше 3, то есть
. Это число немногим больше 2, но меньше 3, то есть 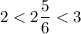 , значит
, значит
В) Так как квадратный корень - это тоже возрастающая функция, то если числа связаны соотношением 0<0,5<1 , то и квадратный корень из этих чисел связан соотношением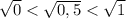 .
.
Так как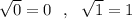 , то
, то 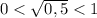 и
и ![\sqrt{0,5}\in [\ 0\ ;\ 1\ ]](/tpl/images/1847/6611/51d25.png) .
.
ответ: №1 .
Г)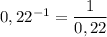
Подберём такие числа, между которыми находится число 0,22 , чтобы легко было разделить единицу на эти числа .
Верно неравенство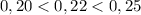 , тогда верно и такое
, тогда верно и такое
неравенство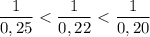 (чем больше знаменатель дроби, тем
(чем больше знаменатель дроби, тем
меньше дробь при равных числителях) , поэтому
ответ: №4 .