хоть 6-7 примеров
первообразная
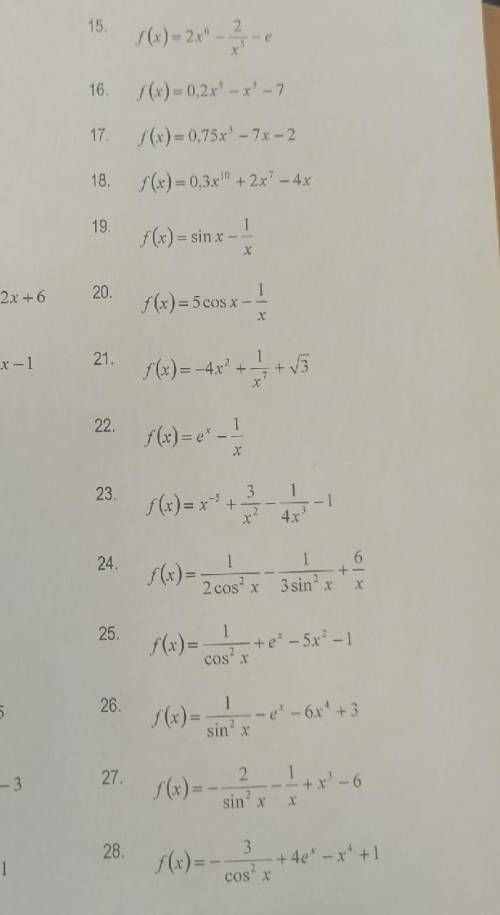
Другие вопросы по теме Математика
Популярные вопросы
- Квадратный стадион сторона которого 150 м посыпан песком сколько надо тачек с...
3 - Что и продолжает людям передавать опыт...
3 - Какой вид связи в словосочетании становилось хорошо...
2 - Классифицировать и назвать формулы: na2so4,ba(oh)2,cd(oh)2,cuso4,agcl,fe(oh)3,bao,sio2,co2,co,so2...
1 - Составьте предложение со словом предложение...
2 - Всаду 120 фруктовых деревьев. из них 50% яблони , 20% груши, остальные вишни....
2 - Реши примеры столбиком: 60: 4 17*5 52: 4 13*5 180: 90...
2 - Неге жылы ауа жоғары көтеріледі? почему теплый воздух поднимается вверх?...
1 - (3x-+2y-3) при x=-3/8 y=1/14 за ранее...
3 - Как будет люк наоборот используя звуки...
1
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.