Математика: HELP! Исследовать сходимость числового ряда!

HELP! Исследовать сходимость числового ряда!

Ответы

Совушка200213 15.10.2020 14:25

Ряд сходится, но не сходится абсолютно

Пошаговое объяснение:

Домножим каждый член ряда на 3, от этого сходимость не поменяется, так что с этого места считаем, что $a_n = \frac{(-1)^{n - 1}}{n}$ .

Заметим, что ряд составленный из $|a_n| = \frac{1}{n}$ является гармоническим рядом, который, как известно, расходится. Поэтому ряд не сходится абсолютно. Чтобы доказать просто сходимость, разобьем слагаемые попарно:

$b_n = a_{2n - 1} + a_{2n}.$

Заметим, что

$b_n = a_{2n - 1} + a_{2n} = \frac{1}{2n - 1} - \frac{1}{2n} = \frac{1}{2n(2n - 1)} \leq \frac{1}{4n^2}.$ Заметим, что ряд составленный из b_n сходится, так как он составлен из положительных членов и мажорируется сходящимся рядом $\frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + ... + \frac{1}{n^2}.$

Обозначим частичные суммы ряда S_n = a_1 + a_2 + ... + a_n .

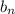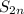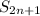Тогда в наших обозначения $S_{2n} = (a_1 + a_2) + ... + (a_{2n - 1} +a_{2n}) = b_1 + b_2 + ... b_n,$ а ряд из b_n сходится, значит $S_{2n}$ имеет предел. Обозначим этот предел за . Для окончания доказательства, докажем что частичные суммы $S_{2n + 1}$ тоже сходятся к a.

$\lim S_{2n + 1} = \lim (S_{2n} + a_{2n + 1}) = \lim S_{2n} + \lim a_{2n + 1} = a + 0$ , так как очевидно, что $\lim a_{n} = 0$ . Итого, мы доказали, что у частичных сумм есть предел , значит ряд сходится по определению